题目内容
9.如图1,在菱形ABCD中,AC=2,BD=2$\sqrt{3}$,AC,BD相交于点O.
(1)求边AB的长;
(2)如图2,将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处,绕点A左右旋转,其中三角板60°角的两边分别与边BC,CD相交于点E,F,连接EF,判断△AEF是哪一种特殊三角形,并说明理由.
分析 (1)利用菱形对角线互相垂直且平分可得AO、OB,根据勾股定理求出即可;
(2)求出△ABE≌△ACF,推出AE=AF,根据有一个角是60°的等腰三角形是等边三角形推出即可.
解答 解:(1)∵在菱形ABCD中,AC=2,BD=2$\sqrt{3}$,
∴∠AOB=90°,OA=$\frac{1}{2}$AC=1,BO=$\frac{1}{2}$BD=$\sqrt{3}$,
在Rt△AOB中,由勾股定理得:AB=$\sqrt{A{O}^{2}+B{O}^{2}}$=2;
(2)△AEF是等边三角形,
理由是:∵由(1)知,菱形ABCD的边长是2,AC=2,
∴△ABC和△ACD是等边三角形,
∴∠BAC=∠BAE+∠CAE=60°,
∵∠EAF=∠CAF+∠CAE=60°,
∴∠BAE=∠CAF,
在△ABE和△ACF中,
$\left\{\begin{array}{l}{∠BAE=∠CAF}\\{AB=AC=2}\\{∠EBA=∠FCA}\end{array}\right.$,
∴△ABE≌△ACF(ASA),
∴AE=AF,
∵∠EAF=60°,
∴△AEF是等边三角形.
点评 本题考查了菱形的性质,全等三角形的性质和判定,等边三角形的性质,以及图形的旋转,题目综合性比较强,有一定的难度.关键是掌握菱形菱形对角线互相垂直且平分.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
4.计算(-3)0的结果为( )
| A. | 0 | B. | 1 | C. | -3 | D. | 3 |
14.在直角坐标系中,点(-2,1)关于原点的对称点是( )
| A. | (-1,2) | B. | (1,2) | C. | (-2,-1) | D. | (2,-1) |
1.为了解学生课外阅读的喜好,某校从六年级随机抽取部分学生进行问卷调查,调查要求每人只选取一种喜欢的书籍,如果没有喜欢的书籍,则作“其他”类统计,图(1)与图(2)是整理数据后绘制的两幅不完整的统计图,以下结论不正确的是( )


| A. | 由这两个统计图不能确定喜欢”小说”的人数 | |
| B. | 若该年级共有1200名学生,则可估计喜爱“科普常识”的学生有360人 | |
| C. | 由这两个统计图可知喜好“科普常识”的学生有90人 | |
| D. | 在扇形统计图中,“漫画”所在扇形的圆心角为72° |
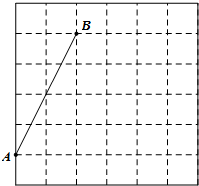 如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上. 如图,直线a,b被直线c所截,若a∥b,∠1=42°,则∠2=138度.
如图,直线a,b被直线c所截,若a∥b,∠1=42°,则∠2=138度.