题目内容
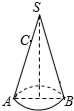 圆锥底面半径为1,高为
圆锥底面半径为1,高为| 15 |
考点:平面展开-最短路径问题,圆锥的计算
专题:
分析:先根据勾股定理求出AS的长,再根据圆锥底面半径为1求出底面的周长,画出圆锥的侧面展开图,根据勾股定理求解即可.
解答: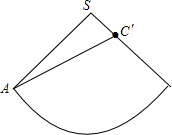 解:如图所示,
解:如图所示,
∵圆锥底面半径为1,高为
,
∴AS=
=4.
∵AC=3,
∴SC=1.
∵圆锥底面半径为1,
∴底面周长=2π,
∴
=2π,解得n=90,
∴∠ASC=90°,
∴蚂蚁所爬行的最短路径长AC′=
=
=
.
故答案为:
.
 解:如图所示,
解:如图所示,∵圆锥底面半径为1,高为
| 15 |
∴AS=
(
|
∵AC=3,
∴SC=1.
∵圆锥底面半径为1,
∴底面周长=2π,
∴
| nπ×4 |
| 180 |
∴∠ASC=90°,
∴蚂蚁所爬行的最短路径长AC′=
| AS2+SC′2 |
| 42+12 |
| 17 |
故答案为:
| 17 |
点评:本题考查的是平面展开-最短路径问题,解答此类问题应先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.一般情况是两点之间,线段最短.在平面图形上构造直角三角形解决问题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
下列各式计算正确的是( )
| A、30=0 | ||
B、3-1=
| ||
C、(2x)-2=
| ||
| D、(x-2)0=1 |
若x1,x2(x1<x2)是关于x的方程(x-a)(x-b)=a-b(a<b)的两个根,则实数x1,x2,a,b的大小关系为( )
| A、x1<x2<a<b |
| B、x1<a<b<x2 |
| C、a<x1<x2<b |
| D、a<x1<b<x2 |
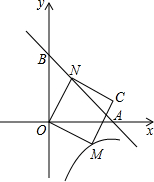 如图,直线y=-x+4交坐标轴于A、B两点,M为反比例函数y=
如图,直线y=-x+4交坐标轴于A、B两点,M为反比例函数y=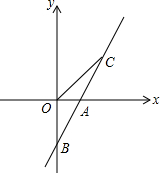 已知:如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2),直线AB上一点C在第一象限,且S△BOC=2.
已知:如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2),直线AB上一点C在第一象限,且S△BOC=2.