题目内容
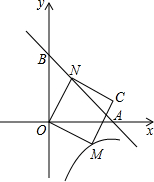 如图,直线y=-x+4交坐标轴于A、B两点,M为反比例函数y=
如图,直线y=-x+4交坐标轴于A、B两点,M为反比例函数y=| -3 |
| x |
考点:反比例函数综合题
专题:
分析:过点N作NE⊥y轴于点E,过点M作MF⊥y轴于点F,如图,易证△NEO≌△OFM,由此可得EN=FO,OE=MF.设点N的坐标为(a,b),则EN=FO=a,OE=MF=b,从而得到点M的坐标为(b,-a),然后把两个点的坐标代入对应的解析式,就可求出a、b的值,从而解决问题.
解答: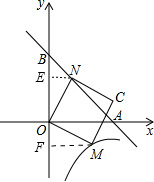 解:过点N作NE⊥y轴于点E,过点M作MF⊥y轴于点F,如图,
解:过点N作NE⊥y轴于点E,过点M作MF⊥y轴于点F,如图,
则有∠NEO=∠MFO=90°.
∵四边形OMCN为正方形,
∴ON=OM,∠NOM=90°,
∴∠NOE=180°-90°-∠FOM=90°-∠FOM=∠FMO.
在△NEO和△OFM中,
,
∴△NEO≌△OFM(AAS),
∴EN=FO,OE=MF.
设点N的坐标为(a,b),
则EN=FO=a,OE=MF=b,
∵点M在第四象限,
∴点M的坐标为(b,-a).
∵M为反比例函数y=
(x>0)上一点,N为直线y=-x+4上一点,
∴
,即
,
解得
或
.
当a=1,b=3时,M点的坐标为(3,-1),N点的坐标为(1,3);
当a=3,b=1时,M点的坐标为(1,-3),N点的坐标为(3,1).
 解:过点N作NE⊥y轴于点E,过点M作MF⊥y轴于点F,如图,
解:过点N作NE⊥y轴于点E,过点M作MF⊥y轴于点F,如图,则有∠NEO=∠MFO=90°.
∵四边形OMCN为正方形,
∴ON=OM,∠NOM=90°,
∴∠NOE=180°-90°-∠FOM=90°-∠FOM=∠FMO.
在△NEO和△OFM中,
|
∴△NEO≌△OFM(AAS),
∴EN=FO,OE=MF.
设点N的坐标为(a,b),
则EN=FO=a,OE=MF=b,
∵点M在第四象限,
∴点M的坐标为(b,-a).
∵M为反比例函数y=
| -3 |
| x |
∴
|
|
解得
|
|
当a=1,b=3时,M点的坐标为(3,-1),N点的坐标为(1,3);
当a=3,b=1时,M点的坐标为(1,-3),N点的坐标为(3,1).
点评:本题主要考查了正方形的性质、全等三角形的判定与性质、直线及反比例函数图象上点的坐标特征、解方程组等知识,构造全等三角形是解决本题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
若x≠0,则
+
=( )
| |x| |
| x |
| x |
| |x| |
| A、-1或1 | B、0 |
| C、1 | D、-2或2 |
下列二次根式中,是最简二次根式的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列方程中是一元二次方程的是( )
| A、2x+1=0 | ||
| B、y2+x=1 | ||
C、x2+
| ||
| D、x2-1=0 |
若等腰三角形的周长为26cm,一边为11cm,则腰长为( )
| A、11cm |
| B、7.5cm或11cm |
| C、7.5cm |
| D、4cm或11cm |
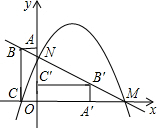 如图,在平面直角坐系中,矩形OABC的顶点A(0,3),C(-1,0).将矩形OABC绕原点顺时针旋转90°,得到矩形OA′B′C′.设直线BB′与x轴交于点M、与y轴交于点N,抛物线y=ax2+2x+c的图象经过点C、M、N.解答下列问题:
如图,在平面直角坐系中,矩形OABC的顶点A(0,3),C(-1,0).将矩形OABC绕原点顺时针旋转90°,得到矩形OA′B′C′.设直线BB′与x轴交于点M、与y轴交于点N,抛物线y=ax2+2x+c的图象经过点C、M、N.解答下列问题: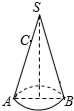 圆锥底面半径为1,高为
圆锥底面半径为1,高为