题目内容
14.已知二次函数y=ax2+bx+1(a<0)的图象过点(1,0)和(x1,0),且-2<x1<-1,下列5个判断中:①b<0;②b-a<0;③a>b-1;④a<-$\frac{1}{2}$;⑤2a<b+$\frac{1}{2}$,正确的是( )| A. | ①③ | B. | ①②③ | C. | ①②③⑤ | D. | ①③④⑤ |
分析 求得与y轴的交点坐标,根据与坐标轴的交点判断出a<0,根据与x轴的交点判定-$\frac{1}{2}$<-$\frac{b}{2a}$<0,从而得出a、b的关系,把(-1,0),(-2,0)代入函数解析式求出a、b、c的关系式,然后对各小题分析判断即可得解.
解答 解:∵抛物线与x轴的交点为(1,0)和(x1,0),-2<x1<-1,与y轴交于正半轴,
∴a<0,
∵-2<x1<-1,
∴-$\frac{1}{2}$<-$\frac{b}{2a}$<0,
∴b<0,b>a,故①正确,②错误;
∵当x=-1时,y>0,
∴a-b+1>0,
∴a>b-1故③正确;
∵由一元二次方程根与系数的关系知x1•x2=$\frac{c}{a}$,
∴x1=$\frac{1}{a}$,
∵-2<x1<-1,
∴-2<$\frac{1}{a}$<-1,
∴-1<a<-$\frac{1}{2}$,故④正确;
∵当x=-2时,y<0,
∴4a-2b+1<0,
∴2a-b<-$\frac{1}{2}$<$\frac{1}{2}$,
∴2a<b+$\frac{1}{2}$,故⑤正确,
综上所述,正确的结论有①③④⑤,
故选:D.
点评 本题考查了二次函数的图象与系数的关系,根据图象与坐标轴的交点坐标判断出a是负数是解题的关键.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
5.若点P(2a-1,3)关于x轴的对称点为Q(3,b),则点M(a,b)关于y轴的对称点的坐标为( )
| A. | (2,-3) | B. | (-2,-3) | C. | (-2,3) | D. | (2,3) |
9. 如图是某几何体的三视图,则该几何体的体积是( )
如图是某几何体的三视图,则该几何体的体积是( )
 如图是某几何体的三视图,则该几何体的体积是( )
如图是某几何体的三视图,则该几何体的体积是( )| A. | 80π | B. | 160π | C. | 640π | D. | 800π |
19. 探索研究:通过对一次函数、反比例函数的学习.我们积累了一定的经验.下面我们借鉴以往研究函数的经验,探索y=$\frac{1}{|x|}$的图象和性质.
探索研究:通过对一次函数、反比例函数的学习.我们积累了一定的经验.下面我们借鉴以往研究函数的经验,探索y=$\frac{1}{|x|}$的图象和性质.
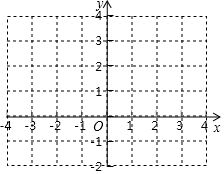
(1)在平面直角坐标系中,画出函数y=$\frac{1}{|x|}$的图象.
①列表填空:
②描点、连线,画出y=$\frac{1}{|x|}$的图象;
(2)结合所画函数图象,写出y=$\frac{1}{|x|}$两条不同类型的性质;
①当x<0时,y随x的增大而增大;②当x>0时,y随x的增大而减小.
知识运用:观察你所画的函数图象,解答下列问题:
(3)若点A(a,c),B(b,c)为该函数图象上不同的两点,则a+b=0.
(4)不等式$\frac{1}{|x|}$>2的解集是-$\frac{1}{2}$<x<0或0<x<$\frac{1}{2}$..
 探索研究:通过对一次函数、反比例函数的学习.我们积累了一定的经验.下面我们借鉴以往研究函数的经验,探索y=$\frac{1}{|x|}$的图象和性质.
探索研究:通过对一次函数、反比例函数的学习.我们积累了一定的经验.下面我们借鉴以往研究函数的经验,探索y=$\frac{1}{|x|}$的图象和性质.(1)在平面直角坐标系中,画出函数y=$\frac{1}{|x|}$的图象.
①列表填空:
| x | … | -3 | -2 | -1 | -$\frac{1}{2}$ | $\frac{1}{2}$ | 1 | 2 | 3 | … |
| y | … | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 2 | 1 | $\frac{1}{2}$ | $\frac{1}{3}$ |
(2)结合所画函数图象,写出y=$\frac{1}{|x|}$两条不同类型的性质;
①当x<0时,y随x的增大而增大;②当x>0时,y随x的增大而减小.
知识运用:观察你所画的函数图象,解答下列问题:
(3)若点A(a,c),B(b,c)为该函数图象上不同的两点,则a+b=0.
(4)不等式$\frac{1}{|x|}$>2的解集是-$\frac{1}{2}$<x<0或0<x<$\frac{1}{2}$..
6.太阳的半径约为696000km,请用科学记数法表示696000这个数,则这个数可记为( )
| A. | 6.96×103 | B. | 69.6×105 | C. | 6.96×105 | D. | -6.96×105 |
4.下列长度的三根小木棒能构成三角形的是( )
| A. | 3cm,3cm,4cm | B. | 7cm,4cm,2cm | C. | 3cm,4cm,8cm | D. | 2cm,3cm,5cm |
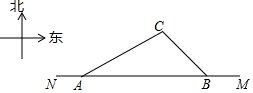 2009年我市荣获“国家卫生城市”称号,是全市人民共同努力的结果,可喜可贺!
2009年我市荣获“国家卫生城市”称号,是全市人民共同努力的结果,可喜可贺!