题目内容
3.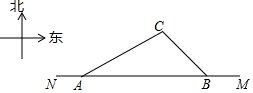 2009年我市荣获“国家卫生城市”称号,是全市人民共同努力的结果,可喜可贺!
2009年我市荣获“国家卫生城市”称号,是全市人民共同努力的结果,可喜可贺!(1)在“创卫”过程中,要在东西方向M、N两地之间修建一条公路,已知:如图,C点周围180m范围内为文物保护区,在MN上点A处测得C在A的北偏东60°方向上,从A向东走500m到达B处,测得C在B的北偏西45°方向上,MN是否穿过文物保护区?为什么?(参考数据:$\sqrt{3}$≈1.732)
(2)在“创卫”过程中,通过拆旧房、植草、栽树、修建公园等措施使城区绿化面积不断增加,2006年年底城区绿化面积为60公顷,计划到2008年年底城区绿化面积达到72.6公顷,试求2007和2008年两年绿化面积的年平均增长率?
分析 (1)作CD⊥AB于点D,设CD=x,由∠CBA=45°知CD=BD=x,由AB=500知AD=500-x,根据tan∠CAD=$\frac{CD}{AD}$列方程求解可得;
(2)设2007和2008年两年绿化面积的年平均增长率为x,根据到2008年年底城区绿化面积达到72.6公顷,列出方程求解可得.
解答 解:(1)过点C作CD⊥AB于点D,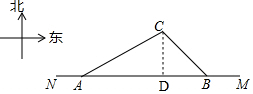
设CD=xm,
∵CD⊥AB,
∴∠CDB=90°,
∵∠CBA=45°,
∴∠DCB=∠CBA=45°,
∴CD=BD=x,
∵AB=500,
∴AD=500-x,
在Rt△ADC中,tan∠CAD=$\frac{CD}{AD}$,
即tan30°=$\frac{x}{500-x}$=$\frac{\sqrt{3}}{3}$,
解得x=$\frac{750(\sqrt{3}-1)}{3}$≈183>180,
∴不会穿过保护区;
(2)设2007和2008年两年绿化面积的年平均增长率为x,
根据题意得:60(1+x)2=72.6,
解得:x1=0.1 x2=-2.1(不符合题意,舍去),
答:2007年和2008年两年绿化面积的年平均增长率为10%.
点评 本题主要考查解直角三角形的应用及一元二次方程的应用,熟练掌握解关于仰角、俯角问题的直角三角形及一元二次方程中关于增长率问题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
14.已知二次函数y=ax2+bx+1(a<0)的图象过点(1,0)和(x1,0),且-2<x1<-1,下列5个判断中:①b<0;②b-a<0;③a>b-1;④a<-$\frac{1}{2}$;⑤2a<b+$\frac{1}{2}$,正确的是( )
| A. | ①③ | B. | ①②③ | C. | ①②③⑤ | D. | ①③④⑤ |
8.下列运算正确的是( )
| A. | (-2a)3=-6a3 | B. | -3a2•4a3=-12a5 | C. | -3a(2-a)=6a-3a2 | D. | 2a3-a2=2a |
15.2sin60°的值等于( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{4}$ | D. | $2\sqrt{3}$ |
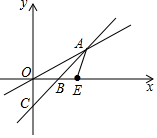 如图,直线y=x-m与直线y=kx(k≠0)交于点A,直线y=x-m与x轴交于点B,与y轴交于点C,若直线y=kx(k≠0)与x轴正半轴所成夹角为30°,OB=$2({\sqrt{3}-1})$.
如图,直线y=x-m与直线y=kx(k≠0)交于点A,直线y=x-m与x轴交于点B,与y轴交于点C,若直线y=kx(k≠0)与x轴正半轴所成夹角为30°,OB=$2({\sqrt{3}-1})$.