题目内容
1.若a<b,且c≠0,用“>,<”号连接下列各式:①a-5<b-5;②a+3<b+3;③7a<7b;④-3a>-3b;
⑤$\frac{a}{{c}^{2}}$<$\frac{b}{{c}^{2}}$;⑥$\frac{a+1}{2}$<$\frac{b+1}{2}$;⑦-$\frac{1}{5}$a+c>-$\frac{1}{5}$b+c;⑧2c-a>-b+2c.
分析 利用不等式性质,直接填空得出答案即可.
解答 解:①a-5<b-5;②a+3<b+3;③7a<7b;④-3a>-3b;
⑤$\frac{a}{{c}^{2}}$<$\frac{b}{{c}^{2}}$;⑥$\frac{a+1}{2}$<$\frac{b+1}{2}$;⑦-$\frac{1}{5}$a+c>-$\frac{1}{5}$b+c;⑧2c-a>-b+2c.
故答案为:<,<,<,>,<,<,>,>.
点评 此题考查不等式的性质,掌握不等式的性质:(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.是解决问题的前提.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.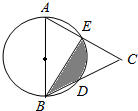 如图,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C.若CE=3,则图中由线段BD,BE和弧DE围成的阴影部分的面积是( )
如图,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C.若CE=3,则图中由线段BD,BE和弧DE围成的阴影部分的面积是( )
 如图,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C.若CE=3,则图中由线段BD,BE和弧DE围成的阴影部分的面积是( )
如图,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C.若CE=3,则图中由线段BD,BE和弧DE围成的阴影部分的面积是( )| A. | $\frac{4}{3}$π-$\sqrt{3}$ | B. | $\frac{3}{2}π$ | C. | $\frac{2}{3}$π-$\sqrt{3}$ | D. | $\frac{8}{3}π$ |
 如图是10×10的网格中,每个方格的边长均为1,刘亮在该网格中标出A,B两点的相对位置,已知点A的位置用(6,2)表示,点B的位置用(9,5)表示.
如图是10×10的网格中,每个方格的边长均为1,刘亮在该网格中标出A,B两点的相对位置,已知点A的位置用(6,2)表示,点B的位置用(9,5)表示.