题目内容
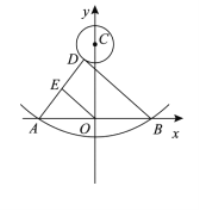
【题目】如图，某校综合实践活动小组的同学欲测量公园内一棵树DE的高度，他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°，朝着这棵树的方向走到台阶下的点C处，测得树顶端D的仰角为60°．已知A点的高度AB为3米，台阶AC的坡度为1：
（即AB：BC=1：），且B、C、E三点在同一条直线上．请根据以上条件求出树DE的高度．
【答案】9米
【解析】
过点A作
于F，可得四边形ABEF为矩形，设
，在
和
中分别表示出CE，BC的长度，求出DF的长度，然后在
中表示出AF的长度，根据
，代入解方程求出x的值即可．
解：如图，过点A作于F，
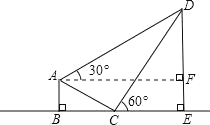
则四边形ABEF为矩形，
，
米，
设，
在
中，
，
在中，
，
，
，
在
中，
，
∴
．
，
，解得
．
答：树DE的高度为9米．
练习册系列答案
相关题目
【题目】参照学习函数的过程与方法，探究函数
的图象与性质．因为
，即
，所以我们对比函数
来探究．
列表：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
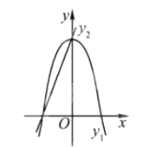
描点：在平面直角坐标系中，以自变量
的取值为横坐标，以相应的函数值为纵坐标，描出相应的点，如图所示：
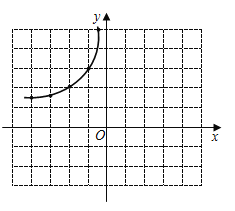
（1）请补全函数图象；
（2）观察图象并分析表格，回答下列问题：
①当
时，
随的增大而_________；（填“增大”或“减小”）
②的图象是由的图象向________平移________个单位而得到；
③图象关于点_________中心对称．（填点的坐标）
（3）结合函数图象，当
时，求的取值范围．
