Question

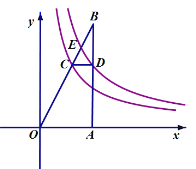
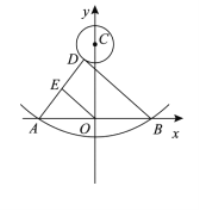
【题目】如图，抛物线与轴交于两点，是以点为圆心，为半径的圆上的动点，是线段的中点，连接，则线段的最小值是（ ）

A.B.C.D.

Answer 1

【答案】A

【解析】

根据抛物线解析式即可得出A点与B点坐标，结合题意进一步可以得出BC长为5，利用三角形中位线性质可知OE=BD，而BD最小值即为BC长减去圆的半径，据此进一步求解即可.

∵，

∴当时，，

解得：，

∴A点与B点坐标分别为：(，0)，(3，0)，

即：AO=BO=3，

∴O点为AB的中点，

又∵圆心C坐标为(0，4)，

∴OC=4，

∴BC长度=，

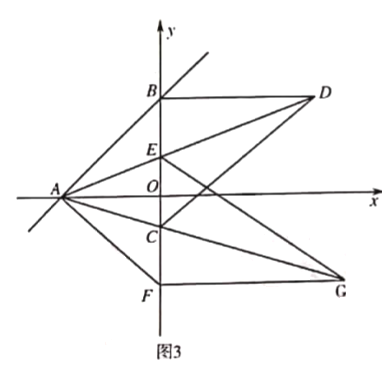
∵O点为AB的中点，E点为AD的中点，

∴OE为△ABD的中位线，

即：OE=BD，

∵D点是圆上的动点，

由图可知，BD最小值即为BC长减去圆的半径，

∴BD的最小值为4，

∴OE=BD=2，

即OE的最小值为2，

故选：A.