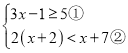题目内容
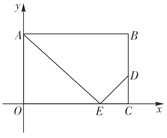
【题目】如图,已知抛物线![]() ,直线
,直线![]() ,当
,当![]() 任取一值时,
任取一值时,![]() 对应的函数值分别 为
对应的函数值分别 为![]() ,若
,若![]() ,取
,取![]() 中的较小值记为
中的较小值记为![]() ;若
;若![]() ,记
,记![]() ,例如:当
,例如:当![]() 时,
时,![]() ,此时
,此时![]() ,下列判断:
,下列判断:
①当![]() 时,
时,![]() ;
;
②当![]() 时,
时,![]() 值越大,
值越大,![]() 值越小;
值越小;
③使得![]() 大于2的
大于2的![]() 值不存在;
值不存在;
④使得![]() 的
的![]() 值是
值是![]() 或
或![]() .
.
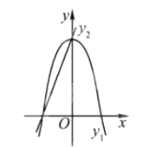
其中正确的是_______________________.
【答案】③④
【解析】
根据二次函数和一次函数的图像与性质即可得出答案.
由题可得,函数图像如图所示
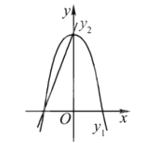
![]()
∴当-1<x<0时,![]() ;当x=-1时,
;当x=-1时,![]() ;当x<-1时,
;当x<-1时,![]() ,故①错误;
,故①错误;
由①可知,当x<0时,抛物线与直线的交点坐标为(-1,0)
结合图示,可知,当-1<x<0时,M=![]() ,当x越大时,M越大;当x=-1时,M=
,当x越大时,M越大;当x=-1时,M=![]() ;当x<-1时,M=
;当x<-1时,M=![]() ,当x越大时,M越大,故②错误;
,当x越大时,M越大,故②错误;
由以上分析可知,当x≥0时,![]() ,则M=
,则M=![]() ,此时
,此时![]() ,故
,故![]() ;当-1<x<0时,M=
;当-1<x<0时,M=![]() ,解得0<M<2;当x≤-1时,M=
,解得0<M<2;当x≤-1时,M=![]() ,解得M≤0,故③正确;
,解得M≤0,故③正确;
由③可得M=1的情况有两种:(1)当x≥0时,即![]() ,解得x=
,解得x=![]() ;(2)当-1<x<0时,2x+2=1,解得x=
;(2)当-1<x<0时,2x+2=1,解得x=![]() ,故④正确;
,故④正确;
故答案为③④.

练习册系列答案
相关题目