题目内容
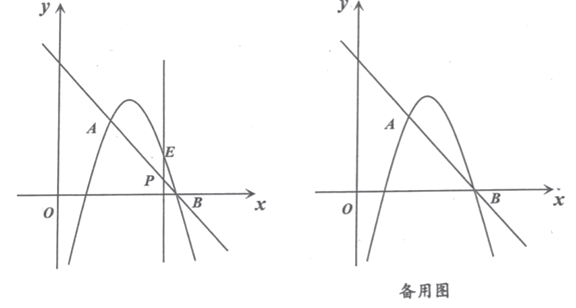
【题目】抛物线![]() 直线
直线![]() 一个交点
一个交点![]() 另一个交点
另一个交点![]() 在
在![]() 轴上,点
轴上,点![]() 是线段
是线段![]() 上异于
上异于![]() 的一个动点,过点
的一个动点,过点![]() 作
作![]() 轴的垂线,交抛物线于点
轴的垂线,交抛物线于点![]() .
.
(1)求抛物线的解析式;
(2)是否存在这样的点![]() ,使线段
,使线段![]() 长度最大?若存在,求出最大值及此时点
长度最大?若存在,求出最大值及此时点![]() 的坐标,若不存在,说明理由;
的坐标,若不存在,说明理由;
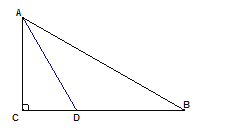
(3)求当![]() 为直角三角形时点P的坐标.
为直角三角形时点P的坐标.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 长度的最大值为
长度的最大值为![]() ,此时点
,此时点![]() 的坐标为
的坐标为![]() ;(3)
;(3)![]() 为直角三角形时点
为直角三角形时点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)根据已知条件先求得![]() ,
,![]() ,将
,将![]() 、
、![]() 坐标代入
坐标代入![]() ,再求得
,再求得![]() 、
、![]() ,最后将其代入
,最后将其代入![]() 即可得解;
即可得解;
(2)假设存在符合条件的点![]() ,并设点
,并设点![]() 的横坐标
的横坐标![]() ,然后根据已知条件用含
,然后根据已知条件用含![]() 的式子表示出
的式子表示出![]() 、
、![]() 的坐标,再利用坐标平面内距离公式求得
的坐标,再利用坐标平面内距离公式求得![]() 、
、![]() 间的距离,将其进行配方即可进行判断并求解;
间的距离,将其进行配方即可进行判断并求解;
(3)分![]() 、
、![]() 两种情况进行讨论,求得相应的符合要求的
两种情况进行讨论,求得相应的符合要求的![]() 点坐标即可.
点坐标即可.
解:(1)∵抛物线![]() 直线
直线![]() 相交于
相交于![]() 、
、![]()
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,则
,则![]()
∴![]() ,
,![]()
∴把![]() 代入
代入![]() 得
得![]()
∴![]()
∴![]()
(2)假设存在符合条件的点![]() ,并设点
,并设点![]() 的横坐标
的横坐标![]()
则![]() 、
、![]()
∴![]()
![]()
![]()
∵![]()
∴![]() 有最大值当
有最大值当![]() 时,
时,![]() 长度的最大值为
长度的最大值为![]() ,此时点
,此时点![]() 的坐标为
的坐标为![]()
(3)①当![]() 时
时
∵直线![]() 垂直于直线
垂直于直线![]()
∴可设直线![]() 的解析式为
的解析式为![]()
∵直线![]() 过点
过点![]()
∴![]()
∴![]()
∴直线![]() 的解析式为
的解析式为![]()
∴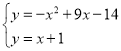
∴![]() 或
或![]() (不合题意,舍去)
(不合题意,舍去)
∴此时点![]() 的坐标为
的坐标为![]()
∴当![]() 时,
时,![]()
∴此时点![]() 的坐标为
的坐标为![]() ;
;
②当![]() 时
时
∴点![]() 的纵坐标与点
的纵坐标与点![]() 的纵坐标相等即
的纵坐标相等即![]()
∴![]()
∴解得![]() (舍去)
(舍去)
∴当![]() 时,
时,![]()
∴此时点![]() 的坐标为
的坐标为![]() .
.
∴综上所述,符合条件的点![]() 存在,
存在,![]() 为直角三角形时点
为直角三角形时点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
故答案是:(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 长度的最大值为
长度的最大值为![]() ,此时点
,此时点![]() 的坐标为
的坐标为![]() ;(3)
;(3)![]() 为直角三角形时点
为直角三角形时点![]() 的坐标为
的坐标为![]() 或
或![]() .
.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案【题目】下表是二次函数![]() 的
的![]() 的部分对应值:
的部分对应值:
| ··· |
|
|
|
|
|
|
| ··· |
| ··· |
|
|
|
|
|
|
| ··· |
则对于该函数的性质的判断:
①该二次函数有最小值;
②不等式![]() 的解集是
的解集是![]() 或
或![]()
③方程![]() 的实数根分别位于
的实数根分别位于![]() 和
和![]() 之间;
之间;
④当![]() 时,函数值
时,函数值![]() 随
随![]() 的增大而增大;
的增大而增大;
其中正确的是:
A.①②③B.②③C.①②D.①③④
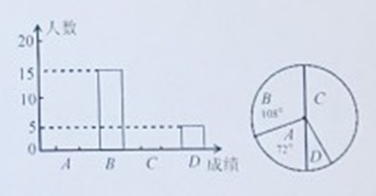
【题目】某校九年级体自模拟测试后,随机抽取了九年级部分学生体有测试成绩进行统计,得到相关的统计图表如下:
成绩/分 |
|
|
|
|
成绩等级 |
|
|
|
|
请根据以上信息解答下列问题:
(1)这次统计共抽取了 名学生的体育测试成绩,补全频数分布直方图
(2)扇形![]() 的圆心角的度数是
的圆心角的度数是
(3)若该校九年级有![]() 名学生,请据此估计该校九年级此次体育测试成绩在
名学生,请据此估计该校九年级此次体育测试成绩在![]() 等级以上(含
等级以上(含![]() 等级)的学生有多少人?
等级)的学生有多少人?
(4)根据测试中存在的问题,通过一段时间的针对性调练,若![]() 等级学生数可提高
等级学生数可提高![]() 等级学生数可提高
等级学生数可提高![]() ,请估计经过训练后九年级体育测试成绩在
,请估计经过训练后九年级体育测试成绩在![]() 等级以上(含
等级以上(含![]() 等级)的学生可达多少人?
等级)的学生可达多少人?