题目内容
18. 如图,△ABC中,∠A=40°,∠ABO=20°,∠ACO=30°,则∠BOC=90°.
如图,△ABC中,∠A=40°,∠ABO=20°,∠ACO=30°,则∠BOC=90°.
分析 根据三角形内角和定理求出∠OBC+∠OCB,根据三角形内角和定理计算即可.
解答 解:∵∠A=40°,∠ABO=20°,∠ACO=30°,
∴∠OBC+∠OCB=180°-40°-20°-30°=90°,
∴∠BOC=180°-(∠OBC+∠OCB)=90°,
故答案为:90°.
点评 本题考查的是三角形内角和定理,掌握三角形内角和等于180°是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.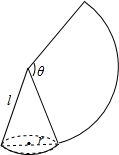 如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,则该圆锥的母线长为( )
如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,则该圆锥的母线长为( )
 如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,则该圆锥的母线长为( )
如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,则该圆锥的母线长为( )| A. | 6cm | B. | 7cm | C. | 8cm | D. | 9cm |
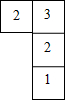 若一个几何体由几个大小相同的小正方体搭成,每个小正方体的棱长为1cm.从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小正方体的个数.
若一个几何体由几个大小相同的小正方体搭成,每个小正方体的棱长为1cm.从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小正方体的个数.