题目内容
12.在中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和1台电子白板需要2万元,购买2台电脑和1台电子白板需要2.5万元.(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共40台,总费用不超过47万元,但不低于45万元,请你通过计算求出有几种购买方案?
分析 (1)根据题意可以列出相应的二元一次方程组,从而可以得到每台电脑、每台电子白板各多少万元;
(2)根据题意可以列出相应的一元一次不等式组,从而可以得到相应的购买方案.
解答 解:(1)设每台电脑x万元,每台电子白板y万元,根据题意得
$\left\{\begin{array}{l}{x+y=2}\\{2x+y=2.5}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{x=0.5}\\{y=1.5}\end{array}\right.$,
即每台电脑0.5万元,每台电子白板1.5万元;
(2)设需购进电脑a台,则购进电子白板(40-a)台,根据题意得
$\left\{\begin{array}{l}{0.5a+1.5(40-a)≤47}\\{0.5a+1.5(40-a)≥45}\end{array}\right.$,
解得,13≤a≤15,
∵a只能取整数,
∴a=13或a=14或a=15,
∴有三种购买方案,
方案一 购进电脑13台,电子白板27台;
方案二 购进电脑14台,电子白板26台;
方案三 购进电脑15台,电子白板25台.
点评 本题考查二元一次方程组的应用、一元一次不等式组的应用,解题的关键是明确题意,列出相应的方程组或不等式组.

练习册系列答案
 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
7.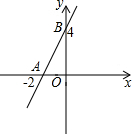 如图,直线y=kx+b交坐标轴于A、B两点,则不等式kx+b>0的解集是( )
如图,直线y=kx+b交坐标轴于A、B两点,则不等式kx+b>0的解集是( )
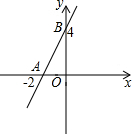 如图,直线y=kx+b交坐标轴于A、B两点,则不等式kx+b>0的解集是( )
如图,直线y=kx+b交坐标轴于A、B两点,则不等式kx+b>0的解集是( )| A. | x>-2 | B. | x>3 | C. | x<-2 | D. | x<3 |
17.下列条件中,能够判定四边形ABCD是平行四边形的是( )
| A. | ∠A=∠C | B. | 对角线AC与BD互相平分 | ||
| C. | AB=CD | D. | 对角线AC与BD互相垂直 |
4.某校广播站招聘一名小记者,小明,小凯,小萍和小芳报名参加了三项测试,成绩如表( )
若把采访写作、计算机操作、创意设计的得分按5:2:3的比例计算三人的最后得分,那么最后得分最高的是( )
| 采访写作 | 计算机操作 | 创意设计 | |
| 小明 | 70 | 60 | 86 |
| 小凯 | 90 | 75 | 51 |
| 小萍 | 60 | 88 | 68 |
| 小芳 | 80 | 70 | 66 |
| A. | 小明 | B. | 小凯 | C. | 小萍 | D. | 小芳 |
1.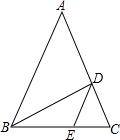 如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,过点D作DE∥AB,交BC于点E,下列结论中错误的是( )
如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,过点D作DE∥AB,交BC于点E,下列结论中错误的是( )
 如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,过点D作DE∥AB,交BC于点E,下列结论中错误的是( )
如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,过点D作DE∥AB,交BC于点E,下列结论中错误的是( )| A. | DE平分∠BDC | B. | △ABC∽△BDC∽△DEC | C. | $\frac{AD}{AB}$=$\frac{\sqrt{5}-1}{2}$ | D. | $\frac{{S}_{△BCD}}{{S}_{△ABD}}$=$\frac{1}{2}$ |
2.下列图形中,不属于中心对称图形的是( )
| A. | 等边三角形 | B. | 菱形 | C. | 矩形 | D. | 平行四边形 |