Question

【题目】如图，直线相交于点，.

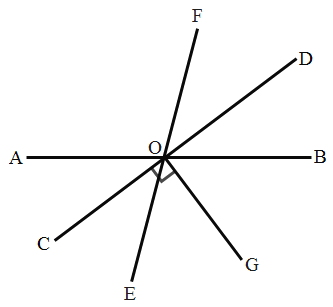
(1)已知，求的度数;

(2)如果是的平分线，那么是的平分线吗?说明理由.

Answer 1

【答案】(1) 51°48′,(2). 是的平分线,理由详见解析.

【解析】

(1)根据平角,直角的性质,解出∠BOG的度数即可.

(2)根据角平分线的性质算出答案即可.

(1)由题意得:∠AOC=38°12′,∠COG=90°,

∴∠BOG=∠AOB-∠AOC-∠COG=180°-38°12′-90°=51°48′.

(2) OG是∠EOB的平分线,理由如下:

由题意得:∠BOG=90°-∠AOC,∠EOG=90°-∠COE,

∵OC是∠AOE的平分线,

∴∠AOC=∠COE

∴∠BOG=90°-∠AOC=90°-∠COE=∠EOG

∴OG是∠EOB的平分线.