Question

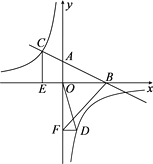
【题目】如图，直线与双曲线交于A，B两点，A点的横坐标为2.

（1）求点B的坐标；

（2）P为线段AB上一点（不包括端点），P点的纵坐标为a，作PN⊥y轴，垂足为N，交双曲线于点M，求的最大值；

Answer 1

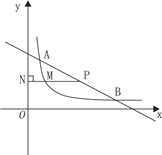
【答案】(1) B（12,1） (2) a=可以取到，所以的最大值为

【解析】(1) 把A点的横坐标为2，代入上，得到A的坐标， 把A的坐标代入，得到k的值．解方程组，即可得到结论．

(2)令y=a，解得，故P(14－2a，a)，M(，a)，得到PN=，MN=．

由PM=PN－MN=，得到，配方即可得到结论．

(1) ∵A点的横坐标为2，A在直线上，∴y==6，∴A(2，6)， 把A(2，6)代入，得：k=12．

，解得：，

∴B（12，1）．

(2)令y=a，，

，∴P(14－2a，a)，

∴M(，a)，∴PN=，MN=．

PM=PN－MN=，

∴．

可以取到，所以的最大值为．