题目内容
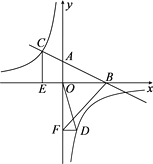
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.
与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.
(1)判断ABC的形状,并说明理由;
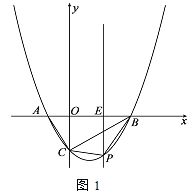
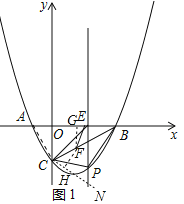
(2)如图1,点P为直线BC下方的二次函数图象上的一个动点(点P与B、C不重合),过点P作y轴的平行线交x轴于点E.当PBC面积的最大值时,点F为线段BC一点(不与点、重合),连接EF,动点G从点E出发,沿线段EF以每秒1个单位的速度运动到点F,再沿FC以每秒![]() 个单位的速度运动到点C后停止,当点F的坐标是多少时,点G在整个运动过程中用时最少?
个单位的速度运动到点C后停止,当点F的坐标是多少时,点G在整个运动过程中用时最少?
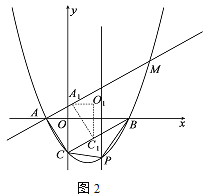
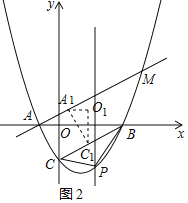
(3)如图2,将ACO沿射线CB方向以每秒![]() 个单位的速度平移,记平移后的ACO为A1C1O1,连接A A1,直线A A1交抛物线与点M,设平移的时间为t秒,当A MC1为等腰三角形时,求t的值.
个单位的速度平移,记平移后的ACO为A1C1O1,连接A A1,直线A A1交抛物线与点M,设平移的时间为t秒,当A MC1为等腰三角形时,求t的值.
【答案】(1)△ABC为直角三角形,理由见解析;(2)![]() ;(3)当△AMC1为等腰三角形时,则t的值t=
;(3)当△AMC1为等腰三角形时,则t的值t=![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】(1)结论:△ABC是直角三角形.在Rt△AOC中,由tan∠ACO=![]() ,推出∠ACO=30°,在Rt△OBC中,由tan∠BCO=
,推出∠ACO=30°,在Rt△OBC中,由tan∠BCO=![]() ,推出∠BCO=60°,可得∠ACB=∠ACO+∠BCO=90°;
,推出∠BCO=60°,可得∠ACB=∠ACO+∠BCO=90°;
(2)设P(m,![]() m2-
m2-![]() m-
m-![]() ),作射线CN,使得∠BCN=60°,作FH⊥CN于H,FG⊥AE于G,则FH=CFcos30°=
),作射线CN,使得∠BCN=60°,作FH⊥CN于H,FG⊥AE于G,则FH=CFcos30°=![]() CF,首先求出点P坐标,动点G的运动时间=
CF,首先求出点P坐标,动点G的运动时间=![]() CF=EF+FH,根据垂线段最短可知,当EH⊥CN时,动点G的运动时间最小,由此即可解决问题;
CF=EF+FH,根据垂线段最短可知,当EH⊥CN时,动点G的运动时间最小,由此即可解决问题;
(3)求出直线AM的解析式,利用方程组求出点M坐标,由题意C′(t,![]() t-
t-![]() ),分三种情形讨论,想办法列出方程即可解决问题;
),分三种情形讨论,想办法列出方程即可解决问题;
(1)结论:△ABC是直角三角形.
理由:如图1中,连接AC.
∵抛物线y=![]() x2-
x2-![]() x-
x-![]() 与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,
与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,
∴A(-1,0),B(3,0),C(0,-![]() ),
),
在Rt△AOC中,∵tan∠ACO=![]() ,
,
∴∠ACO=30°,
在Rt△OBC中,∵tan∠BCO=![]() ,
,
∴∠BCO=60°,
∴∠ACB=∠ACO+∠BCO=90°,
∴△ABC是直角三角形.
(2)设P(m,![]() m2-
m2-![]() m-
m-![]() ),作射线CN,使得∠BCN=60°,作FH⊥CN于H,FG⊥AE于G,则FH=CFcos30°=
),作射线CN,使得∠BCN=60°,作FH⊥CN于H,FG⊥AE于G,则FH=CFcos30°=![]() CF.
CF.
则S△PBC=S△POC+S△POB-S△BOC
=![]() ×
×![]() ×m+
×m+![]() ×3×(-
×3×(-![]() m2+
m2+![]() m+
m+![]() )-
)-![]() ×
×![]() ×3
×3
=-![]() (m-
(m-![]() )2+
)2+ ![]() ,
,
∵-![]() <0,
<0,
∴m=![]() 时,△PBC的面积最大,此时P(
时,△PBC的面积最大,此时P(![]() ,-
,-![]() ),
),
∵动点G的运动时间=![]() CF=EF+FH,
CF=EF+FH,
根据垂线段最短可知,当EH⊥CN时,动点G的运动时间最小,
∵∠EFB=∠EBF=30°,
∴EF=EB=![]() ,
,
在Rt△EFG中,FG=EFcos30°=![]() ,EG=
,EG=![]() ,OG=
,OG=![]() ,
,
∴此时F的坐标为(![]() ,-
,-![]() ).
).
(3)由题意直线BC的解析式为y=![]() x-
x-![]() ,直线AC的解析式为y=
,直线AC的解析式为y=![]() x+
x+![]() ,
,
由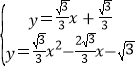 ,
,
解得![]() ,或
,或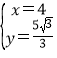
∴M(4,![]() ),
),
∵C1(t,![]() t-
t-![]() ),
),
∴AM2=52+(![]() )2,C1A2=(t+1)2+(
)2,C1A2=(t+1)2+(![]() t-
t-![]() )2,MC1=(4-t)2+(
)2,MC1=(4-t)2+(![]() -
-![]() t+
t+![]() )2,
)2,
①当AM=MC1时,52+(![]() )2=(4-t)2+(
)2=(4-t)2+(![]() -
-![]() t+
t+![]() )2,解得t=5+
)2,解得t=5+![]() 或5-
或5-![]() ,
,
②当C1A=C1M时,(t+1)2+(![]() t-
t-![]() )2=(4-t)2+(
)2=(4-t)2+(![]() -
-![]() t+
t+![]() )2,解得t=
)2,解得t=![]()
③当C1A=AM时,52+(![]() )2=(t+1)2+(
)2=(t+1)2+(![]() t-
t-![]() )2,解得t=
)2,解得t=![]() s或-
s或-![]() (舍弃),
(舍弃),
综上所述,满足条件的t的值为(5+![]() )s或(5-
)s或(5-![]() )s或
)s或![]() s或
s或![]() s.
s.

 口算题天天练系列答案
口算题天天练系列答案【题目】“水是生命之源”,某市自来水公司为了鼓励居民节约用水,规定按以下标准收取水费:
月用水量(吨) | 单价(元/吨) |
不超过25吨 | 1.4 |
超过25吨的部分 | 2.1 |
另:每吨用水加收0.95元的城市污水处理费 | |
(1)如果1月份小明家用水量为18吨,那么小明家1月份应该缴纳水费 元;
(2)小明家2月份共缴纳水费104.5元,那么小明家2月份用水多少吨?
(3)小明家的水表3月份出了故障,只有80%的用水量记入水表中,这样小明家在3月份只缴纳了56.4元水费,问小明家3月份实际应该缴纳水费多少元?