题目内容
【题目】类比、转化等数学思想方法，在数学学习和研究中经常用到，如下是一个案例，请补充完整.
已知
.
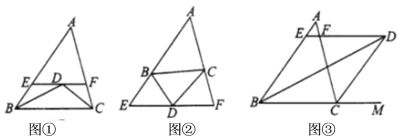
（1）观察发现
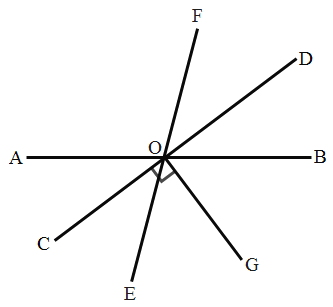
如图①，若点
是
和
的角平分线的交点，过点作
分别交
、
于、
，
填空： 
与
、
的数量关系是________________________________________.
（2）猜想论证
如图②，若点是外角
和
的角平分线的交点，其他条件不变，填： 与、的数量关系是_____________________________________.
（3）类比探究
如图③，若点是和外角
的角平分线的交点.其他条件不变，则（1）中的关系成立吗？若成立，请加以证明；若不成立，请写出关系式，再证明.
【答案】（1）
;（2）;（3）不成立, 
，证明详见解析.
【解析】
（1）根据平行线的性质与角平分线的定义得出∠EDB=∠EBD，∠FCD=∠FDC，从而得出EF与BE、CF的数量关系;
（2）根据平行线的性质与角平分线的定义得出∠EDB=∠EBD，∠FCD=∠FDC，从而得出EF与BE、CF的数量关系;
（3）根据平行线的性质与角平分线的定义得出EF与BE、CF的数量关系．
（1）EF=BE+CF.
∵点D是∠ABC和∠ACB的角平分线的交点，
∴∠EBD=∠DBC，∠FCD=∠DCB．
∵EF∥BC，
∴∠EDB=∠DBC，∠FDC=∠DCB．
∴∠EDB=∠EBD，∠FCD=∠FDC．
∴EB=ED，DF=CF．
∴EF=BE+CF．
故本题答案为：EF=BE+CF．
（2）EF=BE+CF.
∵D点是外角∠CBE和∠BCF的角平分线的交点，
∴∠EBD=∠DBC，∠FCD=∠DCB．
∵EF∥BC，
∴∠EDB=∠DBC，∠FDC=∠DCB．
∴∠EDB=∠EBD，∠FCD=∠FDC．
∴EB=ED，DF=CF．
∴EF=BE+CF．
故本题答案为：EF=BE+CF．
（3）不成立；EF=BECF，证明详见解析．
∵点D是∠ABC和外角∠ACM的角平分线的交点，
∴∠EBD=∠DBC，∠ACD=∠DCM．
∵EF∥BC，
∴∠EDB=∠DBC，∠FDC=∠DCM．
∴∠EBD=∠EDB，∠FDC=∠FCD．
∴BE=ED，FD=FC．
∵EF=EDFD，
∴EF=BECF．
