题目内容
如图,AO是边长为2的等边△ABC的高,点D是AO上的一个动点(点D不与点A、O重合),以CD为一边在AC下方作等边△CDE,连结BE并延长,交AC的延长线于点F.
(1)求证:△ACD≌△BCE;
(2)当△CEF为等腰三角形时,求△CEF的面积.
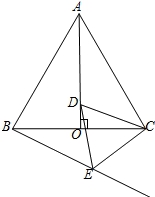
【考点】全等三角形的判定与性质;等腰三角形的性质;等边三角形的性质.
【分析】(1)由△ABC和△CDE是等边三角形,用“SAS”证得△ACD≌△BCE;
(2)首先作CP⊥BF于点P,由∠CBE=30°,求得CP的长,继而求得答案.
【解答】解:(1)∵△ABC为等边三角形
∴AC=BC,∠ACB=60°,
同理可证CD=CE,∠DCE=60°,
∴∠ACB﹣∠DCB=∠DCE﹣∠DCB,
即∠ACD=∠BCE,
在△ACD和△BCE中,
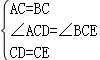 ,
,
∴△ACD≌△BCE(SAS);
(2)由(1)得∠CBE=∠CAD=30°,得△ABF恒为直角三角形,且∠F=30°CF=CB=2,
又因为点D不与点A、O重合,
所以当△CEF为等腰三角形时,∠F只能为顶角,
如图,作CP⊥BF于点P,
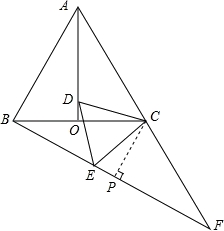
由∠CBE=30°,
得CP=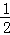 BC=1,
BC=1,
因为CF=EF=2,
所以S△CEF=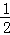 ×2×1=1.
×2×1=1.
【点评】此题考查了全等三角形的判定与性质、等边三角形的性质、等腰三角形的性质以及含30°角的直角三角形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
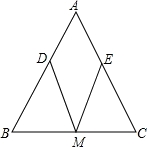
 ,△ABC是等腰三角形.
,△ABC是等腰三角形. 作图痕迹)
作图痕迹)

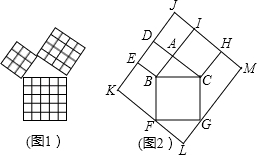
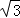 ,PC=1.求∠BPC的度数和等边△ABC的边长.
,PC=1.求∠BPC的度数和等边△ABC的边长. 的图形(如图2).
的图形(如图2).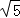 ,BP=
,BP=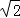 ,PC=1.求∠BPC的度数和正方形ABCD的边长.
,PC=1.求∠BPC的度数和正方形ABCD的边长.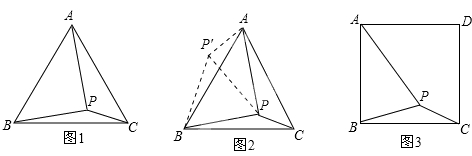
 AB的距离为__________cm.
AB的距离为__________cm.