题目内容
10.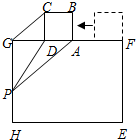 如图,正方形ABCD的边AD与矩形EFGH的边FG重合,将正方形ABCD以lcm/s的速度沿FG方向移动,移动开始前点A与点F重合.在移动过程中,边 AD始终与边FG重合,连接CG,过点A作CG的平行线交线段GH于点P,连接PD.已知正方形ABCD的边长为lcm,矩形EFGH的边FG、GH的长分别为4cm、3cm.设正方形移动时间为x(s),线段GP的长为y (cm),其中0≤x≤2.5.
如图,正方形ABCD的边AD与矩形EFGH的边FG重合,将正方形ABCD以lcm/s的速度沿FG方向移动,移动开始前点A与点F重合.在移动过程中,边 AD始终与边FG重合,连接CG,过点A作CG的平行线交线段GH于点P,连接PD.已知正方形ABCD的边长为lcm,矩形EFGH的边FG、GH的长分别为4cm、3cm.设正方形移动时间为x(s),线段GP的长为y (cm),其中0≤x≤2.5.(1)试求出y关于x的函数关系式,并求当y=3时相应x的值;
(2)记△DGP的面积为S1,ACDG的面积为S2,试说明S1-S2是常数.
分析 (1)根据题意表示出AG、GD的长度,再由△GCD∽△APG,利用对应边成比例可解出x的值.
(2)利用(1)得出的y与x的关系式表示出S1、S2,然后作差即可.
解答 解:(1)∵CG∥AP,
∴∠CGD=∠GAP,
又∵∠CDG=∠AGP,
∴△GCD∽△APG,
∴$\frac{CD}{GD}$=$\frac{PG}{AG}$,
∵GF=4,CD=DA=1,AF=x,
∴GD=3-x,AG=4-x,
∴$\frac{1}{3-x}$=$\frac{y}{4-x}$,即y=$\frac{4-x}{3-x}$,
∴y关于x的函数关系式为y=$\frac{4-x}{3-x}$,
当y=3时,$\frac{4-x}{3-x}$=3,解得x=2.5,
经检验的x=2.5是分式方程的根.
故x的值为2.5;
(2)∵S1=$\frac{1}{2}$GP•GD=$\frac{1}{2}$•$\frac{4-x}{3-x}$•(3-x)=$\frac{4-x}{2}$(cm2),
S2=$\frac{1}{2}$GD•CD=$\frac{1}{2}$(3-x)×1=$\frac{3-x}{2}$(cm2),
∴S1-S2=$\frac{4-x}{2}$-$\frac{3-x}{2}$=$\frac{1}{2}$(cm2),即为常数.
点评 此题考查了正方形的性质、等腰三角形的性质及解直角三角形的知识,解答本题的关键是用移动的时间表示出有关线段的长度,然后运用所学知识进行求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 一飞机A在离地面2400m的上空测得地面控制点B的俯角为60°,求此时飞机与该地面控制点之间的距离.
一飞机A在离地面2400m的上空测得地面控制点B的俯角为60°,求此时飞机与该地面控制点之间的距离. 如图,在矩形ABCD中,AB=8,BC=6,将矩形沿EF折叠,使顶点B与D重合,则折痕EF的长为7.5.
如图,在矩形ABCD中,AB=8,BC=6,将矩形沿EF折叠,使顶点B与D重合,则折痕EF的长为7.5.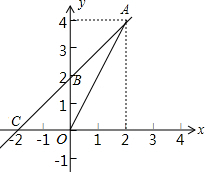 如图,一次函数y=kx+b的图象经过(2,4)、(0,2)两点,与x轴相交于点C.求:
如图,一次函数y=kx+b的图象经过(2,4)、(0,2)两点,与x轴相交于点C.求:
 如图,一个正方体的棱长为2cm,一只蚂蚁欲从A点处沿正方体侧面到B点处吃食物,那么它需要爬行的最短路径的长是2$\sqrt{5}$cm.
如图,一个正方体的棱长为2cm,一只蚂蚁欲从A点处沿正方体侧面到B点处吃食物,那么它需要爬行的最短路径的长是2$\sqrt{5}$cm. 如图,△ABC中,DA=DB,将△CBD沿CD翻折,使B点落在平面ACD内的一点E处.若△ACD与△ECD重叠部分的面积是△ABC的面积的$\frac{1}{4}$,AB=6,求AC的长.
如图,△ABC中,DA=DB,将△CBD沿CD翻折,使B点落在平面ACD内的一点E处.若△ACD与△ECD重叠部分的面积是△ABC的面积的$\frac{1}{4}$,AB=6,求AC的长.