题目内容
阅读：
对于两个不等的非零实数a、b，若分式
的值为零，则x=a或x=b．又因为
=
=x+
-（a+b），所以关于x的方程x+
=a+b有两个解，分别为x1=a，x2=b．
应用上面的结论解答下列问题：
（1）方程x+
=6的两个解中较大的一个为 ；
（2）关于x的方程x+
=
的两个解分别为x1、x2（x1＜x2），若x1与x2互为倒数，则x1= ，x2= ；
（3）关于x的方程2x+
=2n+3的两个解分别为x1、x2（x1＜x2），求
的值．
对于两个不等的非零实数a、b，若分式
| (x-a)(x-b) |
| x |
| (x-a)(x-b) |
| x |
| x2-(a+b)x+ab |
| x |
| ab |
| x |
| ab |
| x |
应用上面的结论解答下列问题：
（1）方程x+
| 8 |
| x |
（2）关于x的方程x+
| m-n |
| mnx |
| m+4mn-n |
| 2mn |
（3）关于x的方程2x+
| n2+2n-3 |
| 2x-1 |
| x2-2 |
| 2x1 |
考点：分式方程的解
专题：阅读型
分析：（1）方程变形后，利用题中的结论确定出较大的解即可；
（2）方程变形后，根据利用题中的结论，以及x1与x2互为倒数，确定出x1与x2的值即可；
（3）方程变形后，根据利用题中的结论表示出为x1、x2，代入原式计算即可得到结果．
（2）方程变形后，根据利用题中的结论，以及x1与x2互为倒数，确定出x1与x2的值即可；
（3）方程变形后，根据利用题中的结论表示出为x1、x2，代入原式计算即可得到结果．
解答：解：（1）方程x+
=6变形得：x+
=2+4，
根据题意得：x1=2，x2=4，
则方程较大的一个解为4；
（2）方程变形得：x+
=
+2，
由题中的结论得：方程有一根为2，另一根为
，
则x1=2，x2=
；
（3）方程整理得：2x-1+
=n-1+n+3，
可到x1=n-1，x2=n+3，
则原式=
=
．
故答案为：（1）4；（2）2；
| 8 |
| x |
| 2×4 |
| x |
根据题意得：x1=2，x2=4，
则方程较大的一个解为4；
（2）方程变形得：x+
| ||
| x |
| m-n |
| 2mn |
由题中的结论得：方程有一根为2，另一根为
| 1 |
| 2 |
则x1=2，x2=
| 1 |
| 2 |
（3）方程整理得：2x-1+
| (n-1)(n+3) |
| 2x-1 |
可到x1=n-1，x2=n+3，
则原式=
| n+3-2 |
| 2n-2 |
| n+1 |
| 2n-2 |
故答案为：（1）4；（2）2；
| 1 |
| 2 |
点评：此题考查了分式方程的解，弄清题中的规律是解本题的关键．
练习册系列答案
相关题目
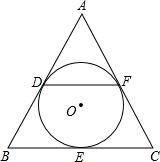如图，△ABC的内切圆⊙O分别和AB，BC，CA切于点D，E，F，∠A=60°，BC=6，△ABC的周长为18，则DF的长为
