题目内容
19. 如图,在菱形ABCD中,AB=10,对角线AC=12.若过点A作AE⊥CD,垂足为E,则AE的长为( )
如图,在菱形ABCD中,AB=10,对角线AC=12.若过点A作AE⊥CD,垂足为E,则AE的长为( )| A. | 9 | B. | $\frac{24}{5}$ | C. | $\frac{48}{5}$ | D. | 9.5 |
分析 连接BD,根据菱形的性质可得AC⊥BD,AO=$\frac{1}{2}$AC,然后根据勾股定理计算出BO长,再算出菱形的面积,然后再根据面积公式DC•AE=$\frac{1}{2}$AC•BD可得答案.
解答 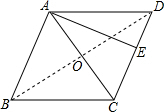 解:连接BD,交AC于O点,
解:连接BD,交AC于O点,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD=10,
∴AC⊥BD,AO=$\frac{1}{2}$AC,BD=2BO,
∴∠AOB=90°,
∵AC=12,
∴AO=6,
∴B0=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∴DB=16,
∴菱形ABCD的面积是$\frac{1}{2}$×AC•DB=$\frac{1}{2}$×12×16=96,
∴DC•AE=96,
解得:AE=$\frac{48}{5}$,
故选:C.
点评 此题主要考查了菱形的性质,以及菱形的性质面积,关键是掌握菱形的对角线互相垂直且平分.

练习册系列答案
相关题目
9.下列图案中,对称轴最多的是( )
| A. |  | B. |  | C. |  | D. |  |
7.下列说法中不正确的是( )
| A. | 若a>b,则a-1>b-1 | B. | 若3a>3b,则a>b | ||
| C. | 若a>b,且c≠0,则ac>bc | D. | 若a>b,则7-a<7-b |
14.若$\sqrt{3}$=a,则$\sqrt{75}$等于( )
| A. | 3a | B. | 5a | C. | 15a | D. | 25a |
4. 如图,边长为1的正方形ABCD绕点A按逆时针方向旋转45°,得到正方形AB′C′D′,正方形ABCD与正方形AB′C′D′叠成一个“风筝”ABCC′D′,那么“风筝”的面积是( )
如图,边长为1的正方形ABCD绕点A按逆时针方向旋转45°,得到正方形AB′C′D′,正方形ABCD与正方形AB′C′D′叠成一个“风筝”ABCC′D′,那么“风筝”的面积是( )
 如图,边长为1的正方形ABCD绕点A按逆时针方向旋转45°,得到正方形AB′C′D′,正方形ABCD与正方形AB′C′D′叠成一个“风筝”ABCC′D′,那么“风筝”的面积是( )
如图,边长为1的正方形ABCD绕点A按逆时针方向旋转45°,得到正方形AB′C′D′,正方形ABCD与正方形AB′C′D′叠成一个“风筝”ABCC′D′,那么“风筝”的面积是( )| A. | 2-$\frac{\sqrt{3}}{3}$ | B. | 3-$\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\frac{7}{4}$ |
11.已知一个矩形的两条对角线夹角为60°,一条对角线长为10cm,则该矩形的周长为( )
| A. | 10(1+$\sqrt{3}$)cm | B. | 20$\sqrt{3}$cm | C. | 20(1+$\sqrt{3}$)cm | D. | 20cm |
9.等腰三角形两边长分别为 5、11,则它的周长为( )
| A. | 21 | B. | 27 | C. | 21 或27 | D. | 不能确定 |
 如图,已知一次函数y=kx+3-2k(k≠0),A(-2,1),C(-2,-3),B(1,-3).
如图,已知一次函数y=kx+3-2k(k≠0),A(-2,1),C(-2,-3),B(1,-3).