题目内容
17.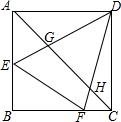 如图,四边形ABCD是正方形,点E、F分别在AB、BC上,∠EDF=45°,DE、DF分别交AC于点G、H.求证:EF=$\sqrt{2}$GH.
如图,四边形ABCD是正方形,点E、F分别在AB、BC上,∠EDF=45°,DE、DF分别交AC于点G、H.求证:EF=$\sqrt{2}$GH.
分析 连接BD,根据四边形ABCD是正方形,于是得到∠DBC=∠CAD=∠ADB=45°,即∠1+∠2=∠2+∠3=45°,求得∠1=∠3,∠DBF=∠DAC,推出△AGD∽△BFD,根据相似三角形的性质得到$\frac{DG}{DF}=\frac{AD}{BD}=\frac{\sqrt{2}}{2}$,延长BA到M,使CF=AM,得到△DFC≌△AMD,根据全等三角形的性质得到∠4=∠5,DF=DM,推出△EDF≌△MDE,根据全等三角形的性质得到∠6=∠8=∠7,证得△DGH∽△DEF,根据相似三角形的性质得到$\frac{GH}{EF}=\frac{DG}{DF}=\frac{\sqrt{2}}{2}$,尽快得到结论.
解答 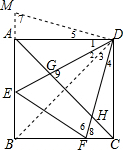 解:连接BD,
解:连接BD,
∵∠EDF=45°,
∵四边形ABCD是正方形,
∴∠DBC=∠CAD=∠ADB=45°,
即∠1+∠2=∠2+∠3=45°,
∴∠1=∠3,∠DBF=∠DAC,
∴△AGD∽△BFD,
∴$\frac{DG}{DF}=\frac{AD}{BD}=\frac{\sqrt{2}}{2}$,
延长BA到M,使CF=AM,
在△DFC与△AMD中,
$\left\{\begin{array}{l}{CF=AM}\\{∠MAD=∠DCF=90°}\\{AD=CD}\end{array}\right.$,
∴△DFC≌△AMD,
∴∠4=∠5,DF=DM,
∵∠EDF=45°,
∴∠1+∠4=45°,
∴∠1+∠5=45°,
在△EDF与△MDE中,
$\left\{\begin{array}{l}{DF=DM}\\{∠EDF=∠MDE}\\{DE=DE}\end{array}\right.$,
∴△EDF≌△MDE,
∴∠6=∠8=∠7,
∴∠8=∠9,
∴∠6=∠9,
∴△DGH∽△DEF,
∴$\frac{GH}{EF}=\frac{DG}{DF}=\frac{\sqrt{2}}{2}$,
∴EF=$\sqrt{2}$GH.
点评 本题考查了全等三角形的判定和性质,相似三角形的判定和性质,正方形的性质,等腰三角形的性质,正确的作出辅助线是解题的关键.

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案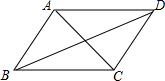 如图,在四边形ABCD中,给出下列的条件,能判断它是平行四边形的是( )
如图,在四边形ABCD中,给出下列的条件,能判断它是平行四边形的是( )| A. | AB∥CD,AD=BC | B. | ∠B=∠C,∠A=∠D | C. | AB=AD,CB=CD | D. | AB=CD,AD=BC |
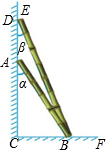 如图,有两根竹竿AB、DB靠在墙角上,并与墙角FCE形成一定的角度,测得∠CAB,∠CDB的度数分别为α,β.用含有α,β的代数式表示∠DBF和∠ABD的度数.
如图,有两根竹竿AB、DB靠在墙角上,并与墙角FCE形成一定的角度,测得∠CAB,∠CDB的度数分别为α,β.用含有α,β的代数式表示∠DBF和∠ABD的度数.