题目内容
8．
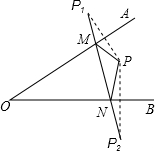如图，点P为∠AOB内一点，分别作出P点关于OA、OB的对称点P1，P2，连接P1P2交OA于M，交OB于N，P1P2=20，则△PMN的周长为20．
分析 根据轴对称的性质可得PM=P1M，PN=P2N，然后求出△PMN的周长=P1P2．
解答 解：∵点P关于OA、OB的对称点P1、P2，
∴PM=P1M，PN=P2N，
∴△PMN的周长=PM+MN+PN=P1M+MN+P2N=P1P2，
∵P1P2=20，
∴△PMN的周长=20．
故答案为：20．
点评 本题考查轴对称的性质，对应点的连线与对称轴的位置关系是互相垂直，对应点所连的线段被对称轴垂直平分，对称轴上的任何一点到两个对应点之间的距离相等，对应的角、线段都相等．
练习册系列答案
特高级教师点拨系列答案
相关题目
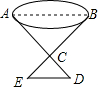如图，要测量池塘两端A、B的距离，可先取一个可以直接到达A和B的点C，连结AC并延长到D，使CD=$\frac{1}{2}$CA，连结BC并延长到E，使CE=$\frac{1}{2}$CB，连结ED．若量出DE的长为25米，则池塘宽AB为50米．
如图，已知△ABD中，∠B=90°，∠D=22.5°，C是BD上一点，AC=CD=8cm．则S△ABC=16cm2．
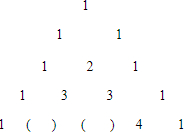（1）观察下列已有的规律，在括号内填上恰当的数．
已知数a，b，c在数轴上的位置如图所示，试化简|a+b|-|b-2|-|c-a|-|2-c|．