题目内容
19. 如图,已知△ABD中,∠B=90°,∠D=22.5°,C是BD上一点,AC=CD=8cm.则S△ABC=16cm2.
如图,已知△ABD中,∠B=90°,∠D=22.5°,C是BD上一点,AC=CD=8cm.则S△ABC=16cm2.
分析 根据等腰三角形的性质得到∠CAD=∠D=22.5°,由外角的性质得到∠ACB=45°,于是得到△ABC 是等腰直角三角形,于是得到结论.
解答 解:∵AC=CD=8cm,
∴∠CAD=∠D=22.5°,
∴∠ACB=45°,
∵∠B=90°,
∴∠BAC=∠ACB,
∴AB=BC=$\frac{\sqrt{2}}{2}$AC=4$\sqrt{2}$,
∴S△ABC=$\frac{1}{2}×$AB•BC=16cm2.
故答案为:16
点评 本题考查了等腰三角形的性质,外角的性质,等腰直角三角形的判定和性质,熟练掌握等腰直角三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
9.参加第十七届韩日世界杯足球赛的23名中国队员的年龄如表所示:
(1)求出年龄最大的队员与年龄最小的队员的年龄差;
(2)求出中国队队员的平均年龄.
| 21 | 29 | 24 | 27 | 33 | 22 | 25 | 25 | 32 | 31 | 28 | 31 |
| 24 | 24 | 23 | 21 | 20 | 27 | 26 | 28 | 23 | 34 | 34 |
(2)求出中国队队员的平均年龄.
14.某校图书馆上周借书记录(超过100册的部分记为正,少于100册的部分记为负)如下表:
(1)上星期五借出多少册书?
(2)上星期借书最多的一天比借书最少的一天多借出图书多少册?
(3)上星期平均每天借出多少册书?
| 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
| +18 | -6 | +15 | 0 | -12 |
(2)上星期借书最多的一天比借书最少的一天多借出图书多少册?
(3)上星期平均每天借出多少册书?
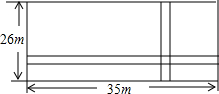 如图,在一块长35m,宽26m的矩形地面上修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),剩余部分栽种花草,要使剩余部分的面积为850m2,道路的宽应该为多少?
如图,在一块长35m,宽26m的矩形地面上修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),剩余部分栽种花草,要使剩余部分的面积为850m2,道路的宽应该为多少?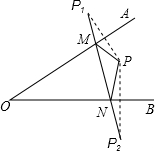 如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=20,则△PMN的周长为20.
如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=20,则△PMN的周长为20. 如图所示,在四边形ABCD中,∠ABC=∠ADC=90°,P是对角线AC的中点,Q是对角线BD的中点,求证:PQ⊥BD.
如图所示,在四边形ABCD中,∠ABC=∠ADC=90°,P是对角线AC的中点,Q是对角线BD的中点,求证:PQ⊥BD.