题目内容
2.某校八年级同学小丽、小强和小红到商场参加了杜会实践活动,在活动中他们参与了某种商品的销售工作.已知该商品的进价为40元/件,下面是他们在活动结束后的对话.小丽:如果以50元/件的价格销售,那么每天可售出100件.
小强:如果以60元/件的价格销售,那么每天可获取利润1600元.
小红:通过调查,我发现每天的销售量y(件)与销售单价x(元)之间存在一次函数关系.
物价部门规定,单件商品利润不低于成本的20%,不高于成本的70%.
(1)求y(件)与x(元)之间的函数关系式.
(2)设该商场销售这种商品每天获取的利润为w元,求出w与x之间的函数关系,并分析当销售单价x为何值时,每天可获得的利润最大,然后求出最大利润的值.
分析 (1)以40元/件的价格销售,那么每天可售出100件;以60元/件的价格销售,那么每天可获取利润1600元.就相当于直线过点(50,100),(60,80),然后列方程组解答即可.
(2)根据利润=销售量×(销售单价-进价)写出解析式,然后利用配方法求最大值.
解答 解:(1)当销售单价为60元/件时,销售量为:$\frac{1600}{60-40}$件,
设y与x的函数关系式为:y=kx+b(k≠0)
把(50,100),(60,80)分别代入得:$\left\{\begin{array}{l}{100=50k+b}\\{80=60k+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-2}\\{b=200}\end{array}\right.$
故y与x的函数关系式为:y=-2x+200(x>0);
(2)∵利润=销售量×(销售单价-进价)
∴W=(-2x+200)(x-40)
=-2x2+280x-8000
=-2(x-70)2+900
∴当销售单价为70元时,每天可获得的利润最大,最大利润是900元.
点评 本题考查了二次函数的应用:先得到二次函数的顶点式y=a(x-h)2+k,当a<0,x=h时,y有最大值k;当a<0,x=h时,y有最小值k.也考查了利用待定系数法求函数的解析式.

练习册系列答案
相关题目
10. 如图,△ABC绕点C按顺时针旋转15°到△DEC,若点A恰好在DE上,AC⊥DE,则∠BAE的度数为( )
如图,△ABC绕点C按顺时针旋转15°到△DEC,若点A恰好在DE上,AC⊥DE,则∠BAE的度数为( )
 如图,△ABC绕点C按顺时针旋转15°到△DEC,若点A恰好在DE上,AC⊥DE,则∠BAE的度数为( )
如图,△ABC绕点C按顺时针旋转15°到△DEC,若点A恰好在DE上,AC⊥DE,则∠BAE的度数为( )| A. | 15° | B. | 55° | C. | 65° | D. | 75° |
 如图,△ABC中,BD=DC=AC,E是DC的中点,求证:AD平分∠BAE.
如图,△ABC中,BD=DC=AC,E是DC的中点,求证:AD平分∠BAE.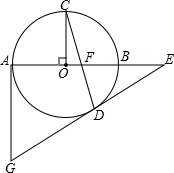 如图,AB是⊙O直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,切线GD与AB延长线交于点E.
如图,AB是⊙O直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,切线GD与AB延长线交于点E. =3
=3 ,则n的值是( )
,则n的值是( )  B.
B.  C.
C.  D.
D. 
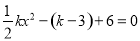 的 两根,则△ABC的周长为( )
的 两根,则△ABC的周长为( )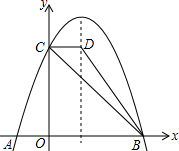 如图,抛物线y=a(x-1)2+4与x轴交于点A,B,与y轴交于点C,过点C作CD∥x轴交抛物线的对称轴于点D,连接BD,已知点A的坐标为(-1,0)
如图,抛物线y=a(x-1)2+4与x轴交于点A,B,与y轴交于点C,过点C作CD∥x轴交抛物线的对称轴于点D,连接BD,已知点A的坐标为(-1,0)