题目内容
17.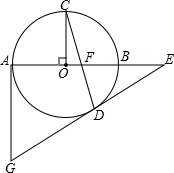 如图,AB是⊙O直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,切线GD与AB延长线交于点E.
如图,AB是⊙O直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,切线GD与AB延长线交于点E.(1)求证:EF=ED;
(2)若AG=3$\sqrt{3}$,⊙O的半径为3,求OF的值.
分析 (1)连接OD,根据切线的性质得OD⊥DE,则∠EDF+∠ODC=90°,而∠C=∠ODC,则∠EDF+∠C=90°,由OC⊥AB,可得∠C+∠OFC=90°,由对顶角性质,等量代换得出∠DFE=∠EDF,得出结论;
(2)先求得EF=ED,设DE=x,则EF=x,根据切线的性质由AG为⊙O的切线得∠ODE=90°,再证明Rt△EOD∽Rt△EGA,利用相似比求得AE,OE,然后根据AE-OE=OA=3,求得x的值,进而求得OF.
解答 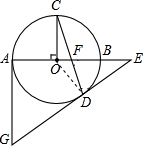 (1)证明:连接OD.
(1)证明:连接OD.
∵DE为⊙O的切线,
∴OD⊥DE,
∴∠ODE=90°,即∠EDF+∠ODC=90°,
∵OC=OD,
∴∠C=∠ODC,
∴∠C+∠EDF=90°,
∵OC⊥AB,
∴∠C+∠OFC=90°,
∵∠OFC=∠DFE,
∴∠C+∠DFE=90°,
∴∠DFE=∠EDF,
∴EF=ED;
(2)解:∵AG,AD为⊙O的切线,
∴DG=AG=3$\sqrt{3}$,
又∵EF=ED,
设DE=x,则EF=x,
∵∠ODE=∠GAE,∠OED=∠GEA,
∴Rt△EOD∽Rt△EGA,
∴$\frac{OD}{AG}$=$\frac{DE}{AE}$=$\frac{OE}{GE}$,即$\frac{3}{3\sqrt{3}}$=$\frac{x}{AE}$=$\frac{OE}{3\sqrt{3}+x}$,
∴AE=$\sqrt{3}$x,OE=3$+\frac{\sqrt{3}}{3}$x,
∵AE-OE=OA=3,
∴$\sqrt{3}$x-(3+$\frac{\sqrt{3}}{3}$x)=3,解得x=3$\sqrt{3}$,
∴AE=$\sqrt{3}$x=9,
∴OF=AE-EF-OA=9-3$\sqrt{3}$-3=6-3$\sqrt{3}$.
点评 本题主要考查了切线的性质和相似三角形的性质,作出适当的辅助线,利用方程思想是解答此题的关键.

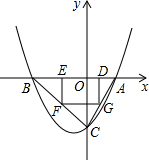 如图,已知抛物线T:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线T上部分点的横坐标对应的纵坐标如下:
如图,已知抛物线T:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线T上部分点的横坐标对应的纵坐标如下:| x | … | -3 | -2 | 1 | 2 | … |
| y | … | -$\frac{5}{2}$ | -4 | -$\frac{5}{2}$ | 0 | … |
(2)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系,并指出m的取值范围;
(3)当矩形DEFG的面积S取最大值m时
①抛物线T上是否存在点P,使S△PBC=m?若存在,请求出P点坐标;若不存在,请说明理由.
②连接DF并延长至点M,使FM=k•DF,若点M不在抛物线T上,求k的取值范围.
超市决定招聘广告策划员一名,某应聘者三项素质测试的成绩如下表所示:
测试项目 | 创新能力 | 综合知识 | 语言表达 |
测试成绩(分) | 82 | 70 | 90 |
将创新能力、综合知识和语言表达三项测试成绩按50%,30%,20%的比例计入总成绩,则该应聘者的总成绩是__________分.
 的结果是( )
的结果是( )