题目内容
6.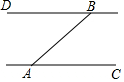 如图,A、B两个码头分别在一条河的两岸AC、BD上,河岸AC、BD均为东西走向,一艘客轮以每小时30千米的速度由A码头出发沿北偏东50°的方向航行至B码头,用时1.2小时,求该河的宽度(结果精确到1千米)
如图,A、B两个码头分别在一条河的两岸AC、BD上,河岸AC、BD均为东西走向,一艘客轮以每小时30千米的速度由A码头出发沿北偏东50°的方向航行至B码头,用时1.2小时,求该河的宽度(结果精确到1千米)【参考数据:sin50°=0.77,cos50°=0.64,tan50°=1.20】
分析 首先过点A作AH⊥BD于点H,进而利用cos∠HAB=$\frac{AH}{AB}$,求出答案即可.
解答  解:过点A作AH⊥BD于点H,
解:过点A作AH⊥BD于点H,
由题意可得:∠HAB=50°,AB=30×1.2=36(m),
在Rt△ABH中,∠AHB=90°,
∵cos∠HAB=$\frac{AH}{AB}$,
∴AH=AB•cos∠HAB=36•cos50°=36×0.64=23.04≈23(m),
答:该河的宽度约为23m.
点评 此题主要考查了解直角三角形的应用,正确应用锐角三角函数关系是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.在“3.15”植树节活动后,对栽下的甲、乙、丙、丁四个品种的树苗进行成活率观测,以下是根据观测数据制成的统计图表的一部分:

请你根据以上信息解答下列问题:
(1)这次栽下的四个品种的树苗共500棵,乙品种树苗100棵;
(2)图1中,甲30%、乙20%,并将图2补充完整;
(3)若经观测计算得出丙种树苗的成活率为89.6%,求这次植树活动的树苗成活率.
| 栽下的各品种树苗棵数统计表 | ||||
| 植树品种 | 甲种 | 乙种 | 丙种 | 丁种 |
| 植树棵数 | 150 | 125 | 125 | |

请你根据以上信息解答下列问题:
(1)这次栽下的四个品种的树苗共500棵,乙品种树苗100棵;
(2)图1中,甲30%、乙20%,并将图2补充完整;
(3)若经观测计算得出丙种树苗的成活率为89.6%,求这次植树活动的树苗成活率.
11.若a2+4a+b2-6b+13=0,则a+b=( )
| A. | 1 | B. | -1 | C. | 5 | D. | -5 |
 如图,一把矩形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,∠ADE=124°,则∠DBC的度数为56°.
如图,一把矩形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,∠ADE=124°,则∠DBC的度数为56°.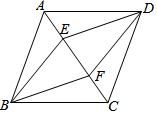 如图,在菱形ABCD中,点E、F在对角线AC上,且AE=CF.
如图,在菱形ABCD中,点E、F在对角线AC上,且AE=CF. 如图,已知三角形ABC,请用直尺和圆规作出∠B的平分线BD,它与边AC相交于点D,并作出BD的中点E.
如图,已知三角形ABC,请用直尺和圆规作出∠B的平分线BD,它与边AC相交于点D,并作出BD的中点E.