题目内容
11．若a2+4a+b2-6b+13=0，则a+b=（ ）| A． | 1 | B． | -1 | C． | 5 | D． | -5 |
分析 由题意a2+4a+b2-6b+13=（a+2）2+（b-3）2，根据非负数的性质分别解出a，b，然后代入a+b进行求解．
解答 解：∵a2+4a+b2-6b+13=（a2+4a+4）+（b2-6b+9）=（a+2）2+（b-3）2=0，
∵（a+2）2≥0，（b-3）2≥0，
∴a+2=0，b-3=0，
∴a=-2，b=3，
∴a+b=-2+3=1．
故选A．
点评 此题考查配方法的应用和非负数的性质，解题的关键是要学会拼凑出完全平方式．
练习册系列答案
相关题目
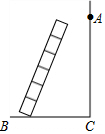如图，墙A处需要维修，A处距离墙脚C处12米，墙下是一条宽BC为5米的小河，现要架一架梯子维修A处的墙体，现有一架14米长的梯子，问这架梯子能否到达墙的A处？
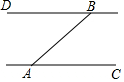如图，A、B两个码头分别在一条河的两岸AC、BD上，河岸AC、BD均为东西走向，一艘客轮以每小时30千米的速度由A码头出发沿北偏东50°的方向航行至B码头，用时1.2小时，求该河的宽度（结果精确到1千米）
如图，长方体底面是长为2cm 宽为1cm的长方形，其高为8cm．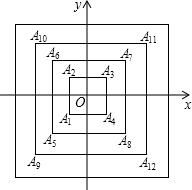
如图，所有正方形的中心均在坐标原点，且各边与x轴或y轴平行．从内到外，它们的边长依次为2，4，6，8，…，顶点依次用A1，A2，A3，A4，…表示，则顶点A51的坐标是（13，13）．