题目内容
如图，点E、F是正方形ABCD对角线AC上的两点，则全等三角形有（ ）
| A、4 | B、5 | C、6 | D、7 |
考点：正方形的性质,全等三角形的判定
专题：
分析：根据正方形的轴对称性写出所有的全等三角形即可．
解答：解：全等三角形有：△ABE≌△ADE，△ABF≌△ADF，△ABC≌△ADC，△BEF≌△DEF，△BEC≌△DEC，△BFC≌△DFC，共6对．
故选C．
故选C．
点评：本题考查了正方形的性质，全等三角形的判定，熟记正方形的对称性是解题的关键，注意确定全等三角形时要按照一定的顺序，做到不重不漏．
练习册系列答案
科学实验活动册系列答案
相关题目
一个袋中装有红、黄、白球各2个，为了确保一次从中取出的球3种颜色都有，则最小要取出（ ）
| A、6个球 | B、5个球 |
| C、4个球 | D、3个球 |
如图，AB∥CD，∠BAC与∠DCA的平分线相交于点G，EG⊥AC于点E，F为AC上的一点，且FA=FG=FC，GH⊥CD于H．下列说法正确的是（ ）①AG⊥CG；②∠BAG=∠CGE；③S△AFG=S△GFC；④若∠EGH：∠ECH=2：7，则∠EGF=50°．
| A、①③④ | B、②③ |
| C、①②③ | D、①②③④ |
如图是一个风景区，A，B，C，D，E，F是这一风景区内的五个主要景点，现观光者聚于A点．假若你是导游，要带领游客欣赏这五个景点后再回到A点，但又不想多走“冤枉路”（不能走重复的路线和经过同一个景点），你认为可选择行走路线有（ ）种．| A、4 | B、5 | C、6 | D、7 |
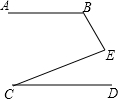如图，若AB∥CD，则∠B、∠C、∠E三者之间的关系是（ ）| A、∠B+∠C+∠E=180° |
| B、∠B+∠E-∠C=180° |
| C、∠B+∠C-∠E=180° |
| D、∠C+∠E-∠B=180° |
如图，在所标识的角中，内错角是（ ）| A、∠1和∠4 |
| B、∠2和∠3 |
| C、∠1和∠3 |
| D、∠3和∠4 |