题目内容
14. 如图:△ABC中,AD是角平分线,AE是高,已知∠B=40°,∠C=70°,求∠DAE的度数.
如图:△ABC中,AD是角平分线,AE是高,已知∠B=40°,∠C=70°,求∠DAE的度数.
分析 根据三角形的内角和定理,可求得∠BAC的度数,由AD是∠BAC的平分线,可得∠DAC的度数;在直角△AEC中,可求出∠EAC的度数,所以∠EAD=∠DAC-∠EAC,即可得出.
解答 解:∵△ABC中,∠B=40°,∠C=70°,
∴∠BAC=180°-∠B-∠C
=180°-40°-70°
=70°,
∵AD是∠BAC的平分线,
∴∠DAC=$\frac{1}{2}$∠BAC=35°,
∵AE是BC边上的高,
∴在直角△AEC中,∠EAC=90°-∠C=90°-70°=20°,
∴∠DAE=∠DAC-∠EAC=35°-20°=15°.
点评 本题主要考查了三角形的内角和定理和三角形的高、角平分线的性质,学生应熟练掌握三角形的高、中线和角平分线这些基本知识,能灵活运用解决问题.

练习册系列答案
相关题目
6.在-5,-$\frac{1}{10}$,-3.5,-0.01,-2,-212各数中,最大的数是( )
| A. | -212 | B. | -$\frac{1}{10}$ | C. | -0.01 | D. | -5 |
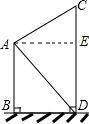 如图,甲楼的底端B处与乙楼的底端D处相距50m,从甲楼顶部A处看乙楼顶部C处的仰角∠CAE的度数为20°.从甲楼顶部A处看乙楼底部D处的俯角∠DAE的度数为35.分别求甲楼AB和乙楼CD的高为多少m(精确到1m).(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
如图,甲楼的底端B处与乙楼的底端D处相距50m,从甲楼顶部A处看乙楼顶部C处的仰角∠CAE的度数为20°.从甲楼顶部A处看乙楼底部D处的俯角∠DAE的度数为35.分别求甲楼AB和乙楼CD的高为多少m(精确到1m).(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)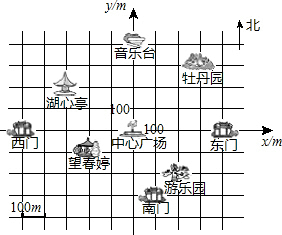 星期天,小明、小刚、小红三名同学到公园玩时走散了,以中心广场为坐标原点,以正东、正北方向为x轴、y轴正方向建立坐标系,他们对着景区示意图通过电话互报出了自己的位置(图中小正方形的边长代表100m).
星期天,小明、小刚、小红三名同学到公园玩时走散了,以中心广场为坐标原点,以正东、正北方向为x轴、y轴正方向建立坐标系,他们对着景区示意图通过电话互报出了自己的位置(图中小正方形的边长代表100m). 如图,小方格都是边长为1的正方形
如图,小方格都是边长为1的正方形