题目内容
4.请先观察下列算式,再填空:32-12=8×1,52-32=8×2.①72-52=8×3;
②92-(7)2=8×4;
③(112)-92=8×5;
④132-(11)2=8×6;
…
(1)通过观察归纳,你知道上述规律的一般形式吗?请把你的猜想写出来.
(2)你能运用本章所学的平方差公式来说明你的猜想的正确性吗?
分析 (1)根据平方差中的第一个奇数表示为2n+1,则第二个奇数表示为2n-1,可以表示出规律的一般形式;
(2)根据平方差公式:(a-b)(a+b)=a2-b2证明即可得到答案.
解答 解:(1)根据各个算式的规律可以得到,
(2n+1)2-(2n-1)2=8n,
(2)证明:(2n+1)2-(2n-1)2=(2n+1+2n-1)(2n+1-2n+1)=8n.
点评 本题考查的是根据算式总结规律和运用平方差公式进行证明的问题,正确表示相应的奇数、熟练运用平方差公式:(a-b)(a+b)=a2-b2是解题的关键.

练习册系列答案
相关题目
 如图,直线BD交AC,AB于D、F,交CB的延长线于E,且$\frac{AD}{DC}$=$\frac{2}{3}$,$\frac{AF}{FB}$=$\frac{7}{3}$,求$\frac{DF}{EF}$的值.
如图,直线BD交AC,AB于D、F,交CB的延长线于E,且$\frac{AD}{DC}$=$\frac{2}{3}$,$\frac{AF}{FB}$=$\frac{7}{3}$,求$\frac{DF}{EF}$的值.
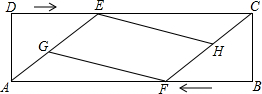 如图,在矩形ABCD中,AB=13cm,AD=4cm,点E、F同时分别从D、B两点出发,以1cm/s的速度沿DC、BA向终点C、A运动,点G、H分别为AE、CF的中点,设运动时间为t(s).
如图,在矩形ABCD中,AB=13cm,AD=4cm,点E、F同时分别从D、B两点出发,以1cm/s的速度沿DC、BA向终点C、A运动,点G、H分别为AE、CF的中点,设运动时间为t(s).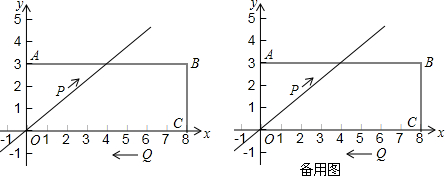
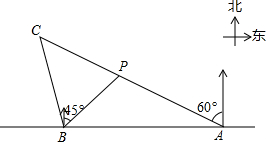 如图,在一笔直的海岸线l上有A、B两个观测站,点A在点B的正东方向,AB=4km,有一艘小船在点P处,从点A 测得小船在北偏西60°方向,从点B测得小船在北偏东45°的方向.
如图,在一笔直的海岸线l上有A、B两个观测站,点A在点B的正东方向,AB=4km,有一艘小船在点P处,从点A 测得小船在北偏西60°方向,从点B测得小船在北偏东45°的方向. 如图:△ABC中,AD是角平分线,AE是高,已知∠B=40°,∠C=70°,求∠DAE的度数.
如图:△ABC中,AD是角平分线,AE是高,已知∠B=40°,∠C=70°,求∠DAE的度数.