题目内容
4.计算$\sqrt{(1-\sqrt{2})^{2}}$-2sin45°+(-2)-3+($π-\sqrt{3}$)0.分析 原式第一项利用二次根式性质化简,第二项利用特殊角的三角函数值计算,第三项利用负整数指数幂法则计算,最后一项利用零指数幂法则计算即可得到结果.
解答 解:原式=$\sqrt{2}$-1-2×$\frac{\sqrt{2}}{2}$-$\frac{1}{8}$+1
=-$\frac{1}{8}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
15.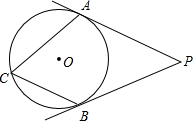 如图,P是⊙O外一点,PA、PB是⊙O的切线,∠APB=50°,点C在⊙O上,则∠ACB=( )
如图,P是⊙O外一点,PA、PB是⊙O的切线,∠APB=50°,点C在⊙O上,则∠ACB=( )
 如图,P是⊙O外一点,PA、PB是⊙O的切线,∠APB=50°,点C在⊙O上,则∠ACB=( )
如图,P是⊙O外一点,PA、PB是⊙O的切线,∠APB=50°,点C在⊙O上,则∠ACB=( )| A. | 50° | B. | 65° | C. | 75° | D. | 130° |
19.下列不等式变形正确的是( )
| A. | 由4x-1≥0得4x>1 | B. | 由5x>3 得 x>3 | C. | 由$\frac{y}{2}$>0得 y>0 | D. | 由-2x<4得x<-2 |
9.下列图形中,既不是轴对称图形,又不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
14.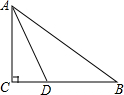 如图,在△ABC中,∠C=90°,AD平分∠CAB,已知CD=3,BD=5,则下列结论中错误的是( )
如图,在△ABC中,∠C=90°,AD平分∠CAB,已知CD=3,BD=5,则下列结论中错误的是( )
 如图,在△ABC中,∠C=90°,AD平分∠CAB,已知CD=3,BD=5,则下列结论中错误的是( )
如图,在△ABC中,∠C=90°,AD平分∠CAB,已知CD=3,BD=5,则下列结论中错误的是( )| A. | AC=6 | B. | AD=7 | C. | BC=8 | D. | AB=10 |
 如图:△ABC中,AD是角平分线,AE是高,已知∠B=40°,∠C=70°,求∠DAE的度数.
如图:△ABC中,AD是角平分线,AE是高,已知∠B=40°,∠C=70°,求∠DAE的度数.