��Ŀ����
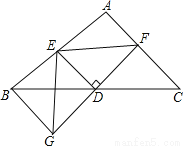
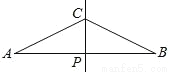
��ͼ��ֱ��CP��AB���д����ҽ�AB��P������AP��2CP���ס�����������AB��ȡ����D��E��ʹ��AD��DC��CE��EB�����������£�
�ף�����ACP����BCP֮��ƽ���ߣ��ֱ�AB��D��E����D��E��Ϊ����
�ң���AC��BC֮�д��ߣ��ֱ�AB��D��E����D��E��Ϊ����
���ڼס������˵������������жϺ�����ȷ��������
A. ���˶���ȷ B. ���˶����� C. ����ȷ���Ҵ��� D. �״�������ȷ
D ����������������� �ס��Ҷ���ȷ�� �����ǣ���CP���߶�AB�Ĵ�ֱƽ���ߣ� ��BC=AC����APC=��BPC=90�㣬 ��AC=2CP�� ���A=30�㣬 ���ACP=60�㣬 ��CDƽ�֡�ACP�� ���ACD=��ACP=30�㣬 ���ACD=��A�� ��AD=DC�� ͬ��CE=BE�� ��D��EΪ���� ��D��A...
��ϰ��ϵ�д�
�����Ŀ


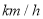 �������ٶ�Ϊ80
�������ٶ�Ϊ80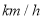 �������Ӽس������쳵���ҵس�����
�������Ӽس������쳵���ҵس�����