题目内容
17.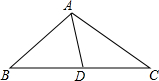 如图,AD是△ABC的中线,∠BAD>∠DAC.求证:AC>AB.
如图,AD是△ABC的中线,∠BAD>∠DAC.求证:AC>AB.
分析 延长AD到E,使DE=AE,连接CE,由AD是△ABC的中线,得到BD=CD,推出△ADB≌△CDE,根据全等三角形的性质得到∠BAD=∠E,AB=CE,由∠BAD>∠DAC,得到∠E>∠CAD,根据三角形的边角关系即可得到结论.
解答 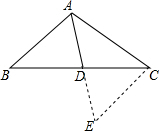 证明:延长AD到E,使DE=AE,连接CE,
证明:延长AD到E,使DE=AE,连接CE,
∵AD是△ABC的中线,
∴BD=CD,
在△ABD与△DEC中,$\left\{\begin{array}{l}{AD=DE}\\{∠ADB=∠CDE}\\{BD=CD}\end{array}\right.$,
∴△ADB≌△CDE,
∴∠BAD=∠E,AB=CE,
∵∠BAD>∠DAC,
∴∠E>∠CAD,
∴AC>CE,
∴AC>AB.
点评 本题考查了全等三角形的判定和性质,三角形的边角关系,正确的作出辅助线构造全等三角形是解题的关键.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
5.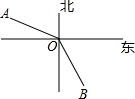 在灯塔O处观测到轮船A位于北偏西65°的方向,同时轮船B在南偏东34°的方向,那么∠AOB的大小为( )
在灯塔O处观测到轮船A位于北偏西65°的方向,同时轮船B在南偏东34°的方向,那么∠AOB的大小为( )
 在灯塔O处观测到轮船A位于北偏西65°的方向,同时轮船B在南偏东34°的方向,那么∠AOB的大小为( )
在灯塔O处观测到轮船A位于北偏西65°的方向,同时轮船B在南偏东34°的方向,那么∠AOB的大小为( )| A. | 69° | B. | 111° | C. | 149° | D. | 159° |
9.已知一次函数y=x+m-3的图象与y轴的交点在x轴上方,则m需满足( )
| A. | m<3 | B. | m≤-3 | C. | m≥3 | D. | m>3 |
 如图,已知等腰三角形ABC的腰长为10,底边BC的长为12,求这个等腰三角形底边上的高AD.
如图,已知等腰三角形ABC的腰长为10,底边BC的长为12,求这个等腰三角形底边上的高AD.