题目内容
14.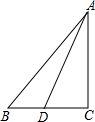 如图,在△ABC中,AD=15,AC=12,DC=9,点B是CD延长线上一点,连接AB,若AB=20.求:△ABD的面积.
如图,在△ABC中,AD=15,AC=12,DC=9,点B是CD延长线上一点,连接AB,若AB=20.求:△ABD的面积.
分析 由勾股定理的逆定理证明△ADC是直角三角形,∠C=90°,再由勾股定理求出BC,得出BD,即可得出结果.
解答 解:在△ADC中,AD=15,AC=12,DC=9,
AC2+DC2=122+92=152=AD2,
即AC2+DC2=AD2,
∴△ADC是直角三角形,∠C=90°,
在Rt△ABC中,BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{2{0}^{2}-1{2}^{2}}$=16,
∴BD=BC-DC=16-9=7,
∴△ABD的面积=$\frac{1}{2}$×7×12=42.
点评 本题考查了勾股定理、勾股定理的逆定理;熟练掌握勾股定理,由勾股定理的逆定理证明三角形是直角三角形是解决问题的关键.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
5.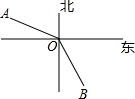 在灯塔O处观测到轮船A位于北偏西65°的方向,同时轮船B在南偏东34°的方向,那么∠AOB的大小为( )
在灯塔O处观测到轮船A位于北偏西65°的方向,同时轮船B在南偏东34°的方向,那么∠AOB的大小为( )
 在灯塔O处观测到轮船A位于北偏西65°的方向,同时轮船B在南偏东34°的方向,那么∠AOB的大小为( )
在灯塔O处观测到轮船A位于北偏西65°的方向,同时轮船B在南偏东34°的方向,那么∠AOB的大小为( )| A. | 69° | B. | 111° | C. | 149° | D. | 159° |
9.已知一次函数y=x+m-3的图象与y轴的交点在x轴上方,则m需满足( )
| A. | m<3 | B. | m≤-3 | C. | m≥3 | D. | m>3 |
 如图共有24个三角形.
如图共有24个三角形.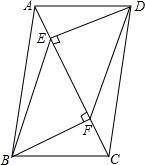 如图,已知AE=CF,AB∥DC,DE⊥AC于点E,BF⊥AC于点F.
如图,已知AE=CF,AB∥DC,DE⊥AC于点E,BF⊥AC于点F.