题目内容
4.解下列方程组(1)$\left\{\begin{array}{l}{x+3y=12①}\\{2x-3y=6②}\end{array}\right.$
(2)$\left\{\begin{array}{l}{3x+y=7①}\\{2x+y=3②}\end{array}\right.$.
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组利用加减消元法求出解即可.
解答 解:(1)①+②得,3x=18,
解得:x=6,
把x=6代入①得,6+3y=12,
解得y=2,
则方程组的解是$\left\{\begin{array}{l}{x=6}\\{y=2}\end{array}\right.$;
(2)①+②得:5x=10,
解得:x=2,
将x=2代入①得:y=1,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
9.某商场用18万购进A、B两种电器,销售完共获利5万元,其进价和售价如表:
(1)该商场购进A、B两种电器各多少台?
(2)商场第二次以原价购进A、B两种电器,购进A电器的台数不变,B电器的台数是第一次的$\frac{1}{2}$;B种电器按原价出售,而A种电器打折销售.若两种电器销售完毕,要使第二次经营获利不少于25000元,A种电器最低售价为每台多少元?
| A | B | |
| 进价(元/台) | 500 | 600 |
| 售价(元/台) | 600 | 790 |
(2)商场第二次以原价购进A、B两种电器,购进A电器的台数不变,B电器的台数是第一次的$\frac{1}{2}$;B种电器按原价出售,而A种电器打折销售.若两种电器销售完毕,要使第二次经营获利不少于25000元,A种电器最低售价为每台多少元?
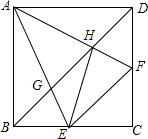 如图,正方形ABCD中,点E,F分别在BC、DC上,∠EAF=45°,AE,AF分别交BD于G,H,下列结论
如图,正方形ABCD中,点E,F分别在BC、DC上,∠EAF=45°,AE,AF分别交BD于G,H,下列结论 如图,AC=AD,BC=BD,求证:△ABC≌△ABD.
如图,AC=AD,BC=BD,求证:△ABC≌△ABD.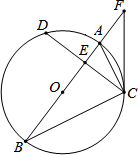 如图,在⊙O中,直径AB平分弦CD、AB与CD相交于点E,连接AC、BC,点F是BA延长线上的一点,且∠FCA=∠B.
如图,在⊙O中,直径AB平分弦CD、AB与CD相交于点E,连接AC、BC,点F是BA延长线上的一点,且∠FCA=∠B.