题目内容
20．以⊙O上任意一点C为圆心，CO长为半径画圆交⊙O于A，B两点，连结OA，OB，CA，CB，则四边形OACB一定是（ ）| A． | 等腰梯形 | B． | 矩形 | C． | 正方形 | D． | 菱形 |
分析 由点和圆的位置关系以及相交两圆的性质得出OA=OC=OB，OC=CA=CB，得出OA=OB=CA=CB，即可得出结论．
解答 解：如图所示：
∵C为⊙O上任意一点，
∴OA=OC=OB，
∵O在⊙C上，
∴OC=CA=CB，
∴OA=OB=CA=CB，
∴四边形OACB是菱形；
故选：D．
点评 本题考查了菱形的判定方法、相交两圆的性质、点和圆的位置关系；熟练掌握相交两圆的性质，证明OA=OB=CA=CB是解决问题的关键．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
10．在3.14、-$\sqrt{2}$、$\root{3}{27}$、π、0.2020020002…这六个数中，无理数有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
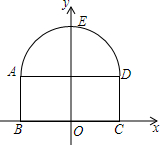如图，隧道的截面由抛物线AED和矩形ABCD构成，矩形的长BC为8m，宽AB为2m，以BC所在的直线为x轴，线段BC的垂直平分线为y轴，建立平面直角坐标系，y轴是抛物线的对称轴，顶点E到坐标原点O的距离为6m．
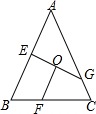如图，在△ABC中，AB=AC，点E、F、G分别在边AB、BC、AC上，CG=BF，BE=CF，O是EG的中点，求证：FO⊥GE．