题目内容
15．
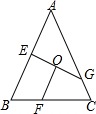如图，在△ABC中，AB=AC，点E、F、G分别在边AB、BC、AC上，CG=BF，BE=CF，O是EG的中点，求证：FO⊥GE．
分析 连接EF，FG，利用SAS证明△BEF与△CFG全等，再利用等腰三角形的性质证明即可．
解答 证明：连接EF，FG，如图：
∵AB=AC，
∴∠B=∠C，
在△BEF与△CFG中，
$\left\{\begin{array}{l}{BE=CF}\\{∠B=∠C}\\{BF=CG}\end{array}\right.$，
∴△BEF≌△CFG（SAS），
∴EF=FG，
∵O是EG的中点，
∴FO⊥GE．
点评 本题考查的是全等三角形的判定与性质，熟知全等三角形的SAS、ASA、SSS及HL定理是解答此题的关键．
练习册系列答案
相关题目
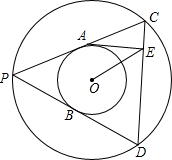如图，以O为圆心的两个同心圆，大圆半径为5，小圆半径为$\sqrt{5}$，点P为大圆上的一点，PC、PB切小圆于点A、点B，交大圆于C、D两点，点E为弦CD上任一点，则AE+OE的最小值为$\sqrt{53}$．
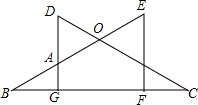如图，已知CD=BE，DG⊥BC于点G，EF⊥BC于点F，且DG=EF．
20．以⊙O上任意一点C为圆心，CO长为半径画圆交⊙O于A，B两点，连结OA，OB，CA，CB，则四边形OACB一定是（ ）
| A． | 等腰梯形 | B． | 矩形 | C． | 正方形 | D． | 菱形 |
一个小立方块的六个面分别标有数字1，2，3，4，5，6，从三个不同方向看到的情形如图所示，则如图放置时三个底面上的数字之和等于（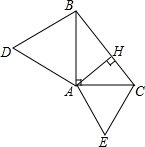
△ABC中，∠BAC=90°，分别以AB、AC为边，得到等边△ABD、等边△ACE．过A作AH⊥BC于点H．求证：