题目内容
9．在四边形ABCD中，∠BAC=90°，AB∥CD，请你添上一个条件：AB=CD，使得四边形ABCD是矩形．分析 AB=CD，根据平行四边形的判定得出四边形ABCD是平行四边形，再根据矩形的判定得出即可．
解答 解：AB=CD，
理由是：∵AB∥CD，AB=CD，
∴四边形ABCD是平行四边形，
∵∠BAC=90°，
∴四边形ABCD是矩形，
故答案为：AB=CD．
点评 本题考查了矩形的判定和平行四边形的判定，能熟记矩形的判定定理是解此题的关键．
练习册系列答案
相关题目
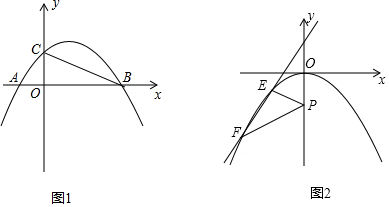
19．在平面直角坐标系中，抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A、B两点（点A在点B的左侧），点M为顶点，连接OM，若y与x的部分对应值如表所示：
（1）求抛物线的解析式；
（2）抛物线与y轴交于点C，点Q是直线BC下方抛物线上一点，点Q的横坐标为xQ．若S△BCQ≥$\frac{1}{2}$S△BOC，求xQ的取值范围；
（3）如图2，平移此抛物线使其顶点为坐标原点，P（0，-1）为y轴上一点，E为抛物线上y轴左侧的一个动点，从E点发出的光线沿EP方向经过y轴上反射后与此抛物线交于另一点F．则当E点位置变化时，直线EF是否经过某个定点？如果是，请求出此定点的坐标；若不是，请说明理由．
| x | … | -1 | 0 | 3 | … |
| y | … | 0 | 3/2 | 0 | … |
（2）抛物线与y轴交于点C，点Q是直线BC下方抛物线上一点，点Q的横坐标为xQ．若S△BCQ≥$\frac{1}{2}$S△BOC，求xQ的取值范围；
（3）如图2，平移此抛物线使其顶点为坐标原点，P（0，-1）为y轴上一点，E为抛物线上y轴左侧的一个动点，从E点发出的光线沿EP方向经过y轴上反射后与此抛物线交于另一点F．则当E点位置变化时，直线EF是否经过某个定点？如果是，请求出此定点的坐标；若不是，请说明理由．
17．如果$\sqrt{{a}^{2}}$=-a，那么a的取值范围是（ ）
| A． | 正数 | B． | 负数 | C． | 非负数 | D． | 非正数 |
4．若（am+1bn+2）•（-a2n-1b2m）=-a3b5，则m+n的值为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | -3 |
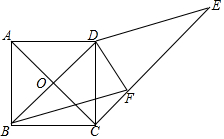如图，正方形ABCD的边长为1，对角线交于点O，作∠DBF=30°，CE∥BD，DE∥BF，CE与BF交于点F，连接DF，∠DFC=105°．
19．下列图形中，是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |