题目内容
9.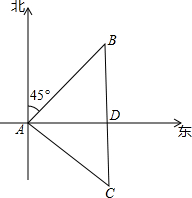 如图,小明先从A地沿东北方向走100$\sqrt{2}$m,到达B地向正南方向走200m到达C地,
如图,小明先从A地沿东北方向走100$\sqrt{2}$m,到达B地向正南方向走200m到达C地,(1)此时小明离A地多远?
(2)小明在A地的什么地方?
分析 (1)在直角△ABD中利用三角函数求得AD和BD的长,则CD即可求得,再在直角△ACD中利用勾股定理求解;
(2)利用三角函数求得∠DAC的度数即可确定.
解答 解:(1)△ABD中,∠BAD=45°,
则BD=AB•sin45=100$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=100(m),AD=BD=100(m).
则CD=BC-BD=200-100=100(m),
在△ACD中,AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{10{0}^{2}+10{0}^{2}}$=100$\sqrt{2}$(m).
则此时到A的距离是100$\sqrt{2}$m;
(2)tan∠DAC=$\frac{CD}{AD}$=$\frac{100}{100}$=1,则∠DAC=45°.
则小明在A的南偏东45°.
点评 本题考查了方向角和勾股定理以及三角函数,理解解直角三角形的条件是关键.

练习册系列答案
相关题目
19.已知菱形的周长是16,一边上的高是6,则菱形的面积是( )
| A. | 12 | B. | 24 | C. | 48 | D. | 64 |
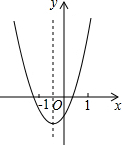 二次函数y=ax2+bx+c的图象如图所示,下列结论:①abc<0;②2a-b<0;③a+b+c>0;④a-b+c<0;其中正确的有( )
二次函数y=ax2+bx+c的图象如图所示,下列结论:①abc<0;②2a-b<0;③a+b+c>0;④a-b+c<0;其中正确的有( )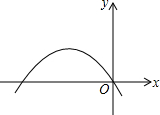 如图的抛物线是二次函数y=ax2-3x+a2-1的图象,那么a的值是-1,抛物线对称轴为直线x=-$\frac{3}{4}$,顶点是(-$\frac{3}{4}$,$\frac{9}{16}$).
如图的抛物线是二次函数y=ax2-3x+a2-1的图象,那么a的值是-1,抛物线对称轴为直线x=-$\frac{3}{4}$,顶点是(-$\frac{3}{4}$,$\frac{9}{16}$). 如图,在△ABC中,AB的垂直平分线交AC于点D,交AB于点E,BD+DC=10cm,求AC的长.
如图,在△ABC中,AB的垂直平分线交AC于点D,交AB于点E,BD+DC=10cm,求AC的长.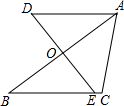 如图,在△ABC中,点O为AB的中点,AD∥BC,过点O的直线交AD,BC于点D,E.求证:OD=OE.
如图,在△ABC中,点O为AB的中点,AD∥BC,过点O的直线交AD,BC于点D,E.求证:OD=OE.