题目内容
17.已知y=y1+y2,y1与x-1成正比例,y2与x成反比例,并且当x=1时,y=2,x=2时,y=4,求y与x之间的函数关系式.分析 设y1=k(x-1),y2=$\frac{m}{x}$,则y=k(x-1)+$\frac{m}{x}$,然后把x和对应的y的值代入得到关于m、k的方程组求解.
解答 解:设y1=k(x-1),y2=$\frac{m}{x}$,
则y=k(x-1)+$\frac{m}{x}$,
根据题意得:$\left\{\begin{array}{l}{m=2}\\{k+\frac{m}{2}=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=2}\\{k=3}\end{array}\right.$,
则y与x的函数数关系式是y=2(x-1)+$\frac{2}{m}$.
点评 本题考查了待定系数法求函数的解析式,理解成正比例、反比例的含义是解决本题的关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
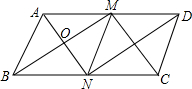 如图,在?ABCD中,M,N分别是AD,BC的中点,连接AN,BM,CM,DN,AN与BM交于点O.
如图,在?ABCD中,M,N分别是AD,BC的中点,连接AN,BM,CM,DN,AN与BM交于点O. 如图,在Rt△ABC中,AC=5,BC=12,将Rt△ABC沿AD折叠后,使点C落在AB上的点E处,求CD.
如图,在Rt△ABC中,AC=5,BC=12,将Rt△ABC沿AD折叠后,使点C落在AB上的点E处,求CD. 如图,在△ABC中,∠A=60°,BC=10,BO平分∠ABC,CO平分∠ACB,MN经过点O与AB,AC相交于点M,N,且MN∥BC,△AMN的周长为18.
如图,在△ABC中,∠A=60°,BC=10,BO平分∠ABC,CO平分∠ACB,MN经过点O与AB,AC相交于点M,N,且MN∥BC,△AMN的周长为18. 如图,四边形ABCD中,AB=DC,∠A=∠D,M、N分别是AD、BC的中点,E、F分别是BM、CM的中点,求证:四边形MENF是菱形.
如图,四边形ABCD中,AB=DC,∠A=∠D,M、N分别是AD、BC的中点,E、F分别是BM、CM的中点,求证:四边形MENF是菱形.