题目内容
10.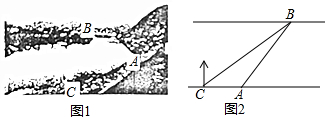 如图1,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走50m到达C点,测得点B在点C的北偏东60°方向,如图2,求出这段河的宽(结果精确到1m,备用数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73).
如图1,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走50m到达C点,测得点B在点C的北偏东60°方向,如图2,求出这段河的宽(结果精确到1m,备用数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73).
分析 作BD⊥CA,由CD=$\frac{BD}{tan∠BCD}$=$\sqrt{3}$x、AD=BD=x,根据AC+AD=CD可得50+x=$\sqrt{3}$x,解之即可得.
解答 解:如图,作BD⊥CA,交CA延长线于点D,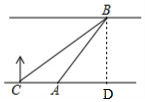
设BD=xm,
∵∠BCA=30°,
∴CD=$\frac{BD}{tan∠BCD}$=$\frac{x}{\frac{\sqrt{3}}{3}}$=$\sqrt{3}$x,
∵∠BAD=45°,
∴AD=BD=x,
由AC+AD=CD可得50+x=$\sqrt{3}$x,
解得:x=$\frac{50}{\sqrt{3}-1}$=25+25$\sqrt{3}$≈68(m),
答:这段河的宽约为68m.
点评 本题主要考查解直角三角形的应用-仰角俯角问题,解题的关键是熟练掌握三角函数的定义表示出各线段的长,根据线段间的关系建立方程.

练习册系列答案
相关题目
1.二次函数y=2x2-2x+m(0<m<$\frac{1}{2}$),如果当x=a时,y<0,那么当x=a-1时,函数值y的取值范围为( )
| A. | y<0 | B. | 0<y<m | C. | m<y<m+4 | D. | y>m |
18.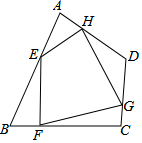 如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )
如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )
 如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )
如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )| A. | 当E,F,G,H是各边中点,且AC=BD时,四边形EFGH为菱形 | |
| B. | 当E,F,G,H是各边中点,且AC⊥BD时,四边形EFGH为矩形 | |
| C. | 当E,F,G,H不是各边中点时,四边形EFGH可以为平行四边形 | |
| D. | 当E,F,G,H不是各边中点时,四边形EFGH不可能为菱形 |
19.已知二次函数y=ax2-ax(a为常数,且a≠0),图象的顶点为C.以下三个结论:①无论a为何值,该函数的图象与x轴一定有两个交点;②无论a为何值,该函数的图象在x轴上截得的线段长为2;③若该函数的图象与x轴有两个交点A、B,且S△ABC=1时,则a=8.其中正确的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
20.下列计算正确的是( )
| A. | 3m-m=2 | B. | m4÷m3=m | C. | (-m2)3=m6 | D. | -(m-n)=m+n |
 如图,四边形ABCD中,∠A=∠ABC=90°,AD=10cm,BC=30cm,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.
如图,四边形ABCD中,∠A=∠ABC=90°,AD=10cm,BC=30cm,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.