题目内容
15.已知一次函数y=kx+m的图象经过点A(0,1),且k=$\frac{b+c}{a}$=$\frac{a+c}{b}$=$\frac{a+b}{c}$,求这个一次函数的表达式.分析 由图象经过点A(0,1)知m=1,根据k=$\frac{b+c}{a}$=$\frac{a+c}{b}$=$\frac{a+b}{c}$可得(a+b+c)k=2(a+b+c),分a+b+c≠0、a+b+c=0两种情况分别求出k的值即可的直线解析式.
解答 解:∵一次函数y=kx+m的图象经过点A(0,1),
∴m=1,
∵k=$\frac{b+c}{a}$=$\frac{a+c}{b}$=$\frac{a+b}{c}$,
∴ak=b+c ①,bk=a+c ②,ck=a+b ③,
①+②+③,得:ak+bk+ck=b+c+a+c+a+b,
即(a+b+c)k=2(a+b+c),
当a+b+c≠0时,k=2,
∴一次函数的表达式为:y=2x+1;
当a+b+c=0时,b+c=-a=ak,解得:k=-1;
∴一次函数的表达式为:y=-x+1;
综上,一次函数的表达式为:y=2x+1或y=-x+1.
点评 本题主要考查一次函数表达式求法,根据题意求出k的值是解题的切入点,根据a+b+c是否为0分类讨论是解题的关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
5.在数-3.8,-10,$-|{-\frac{20}{7}}|$,π,3.14159中,分数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7. 如图,点O为平行四边形ABCD对角线AC、BD的交点,过点O的直线与边AB、DC的延长线分别交于点E、F,EF与AD、BC相交于点G、H.则图中全等三角形有( )
如图,点O为平行四边形ABCD对角线AC、BD的交点,过点O的直线与边AB、DC的延长线分别交于点E、F,EF与AD、BC相交于点G、H.则图中全等三角形有( )
 如图,点O为平行四边形ABCD对角线AC、BD的交点,过点O的直线与边AB、DC的延长线分别交于点E、F,EF与AD、BC相交于点G、H.则图中全等三角形有( )
如图,点O为平行四边形ABCD对角线AC、BD的交点,过点O的直线与边AB、DC的延长线分别交于点E、F,EF与AD、BC相交于点G、H.则图中全等三角形有( )| A. | 8对 | B. | 9对 | C. | 10对 | D. | 11对 |
5.若m等于它的倒数,则分式$\frac{{m}^{2}-4m+4}{{m}^{2}-4}÷(m-2)$的值为( )
| A. | $\frac{1}{3}$ | B. | 1 | C. | $\frac{1}{3}$或1 | D. | 以上都不对 |




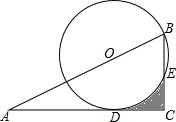 在Rt△ABC中,∠C=90°,∠A=30°,O在斜边AB上,半径为4cm的圆O过点B,切AC于点D,交BC于点E.
在Rt△ABC中,∠C=90°,∠A=30°,O在斜边AB上,半径为4cm的圆O过点B,切AC于点D,交BC于点E.