题目内容
19.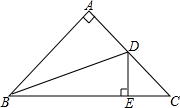 如图,在△ABC中,∠BAC=90°,AB=AC,点D为边AC的中点,DE⊥BC于点E,连接BD,则tan∠DBC的值为$\frac{1}{3}$.
如图,在△ABC中,∠BAC=90°,AB=AC,点D为边AC的中点,DE⊥BC于点E,连接BD,则tan∠DBC的值为$\frac{1}{3}$.
分析 利用等腰直角三角形的判定与性质得出BC=$\sqrt{2}$AC,DE=EC=$\frac{\sqrt{2}}{2}$DC,然后通过解直角△DBE来求tan∠DBC的值即可.
解答 解:∵在△ABC中,∠BAC=90°,AB=AC,
∴∠ABC=∠C=45°,BC=$\sqrt{2}$AC.
又∵点D为边AC的中点,
∴AD=DC=$\frac{1}{2}$AC.
∵DE⊥BC于点E,
∴∠CDE=∠C=45°,
∴DE=EC=$\frac{\sqrt{2}}{2}$DC=$\frac{\sqrt{2}}{4}$AC.
∴tan∠DBC=$\frac{DE}{BE}$=$\frac{\frac{\sqrt{2}}{4}AC}{\sqrt{2}AC-\frac{\sqrt{2}}{4}AC}$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查了解直角三角形的应用、等腰直角三角形的性质.通过解直角三角形,可求出相关的边长或角的度数或三角函数值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.若$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$是方程x-ky=0的解,则k的值为( )
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | -$\frac{2}{3}$ | D. | $\frac{2}{3}$ |
7.一个正多边形的每个内角比相邻外角大36°,则这个多边形是正( )边形.
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
14.某班七个合作学习小组人数如下:4,5,5,x,6,7,8,已知这组数据的平均数为6,则这组数据的中位数和众数是( )
| A. | 5,5 | B. | 6,5 | C. | 6,5和6 | D. | 6,5和7 |