题目内容
4．如果2a2m-5b4与mab3n-2是同类项，那么m=3，n=2．分析 依据同类项的定义可知2m-5=1，3n-2=4，从而可求得m、n的值．
解答 解：∵2a2m-5b4与mab3n-2是同类项，
∴2m-5=1，3n-2=4．
∴m=3，n=2．
故答案为：3；2．
点评 本题主要考查的是同类项的定义，由同类项的定义得到2m-5=1，3n-2=4是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
15．一次函数y=（k-3）x+9与一次函数y=-x+2的图象平行，则k=（ ）
| A． | 2 | B． | $\frac{5}{2}$ | C． | $\frac{7}{2}$ | D． | 4 |
12．下列变形正确的是（ ）
| A． | 4x-5=3x+2变形得4x-3x=-2+5 | B． | $\frac{18+x}{3}$=x-1去分母得18+x=3x-1 | ||
| C． | 3（x-1）=2（x+3）变形得3x-3=2x+6 | D． | 3x=2变形得x=$\frac{3}{2}$ |
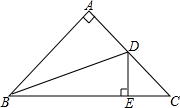如图，在△ABC中，∠BAC=90°，AB=AC，点D为边AC的中点，DE⊥BC于点E，连接BD，则tan∠DBC的值为$\frac{1}{3}$．
16．
如图，线段AB上有2个点C、D，则以这4个点为端点的线段的条数是（ ）
如图，线段AB上有2个点C、D，则以这4个点为端点的线段的条数是（ ）| A． | 4 | B． | 5 | C． | 6 | D． | 7 |