Question

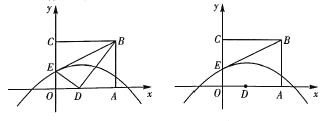
【题目】如图，抛物线与轴交于，两点，与轴交于点，抛物线的对称轴与轴交于点，顶点坐标为.

（1）求抛物线的表达式和顶点的坐标；

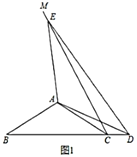
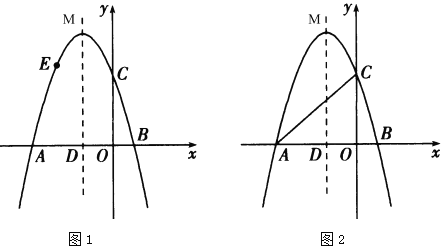
（2）如图1，点为抛物线上一点，点不与点重合，当时，过点作轴，交抛物线的对称轴于点，作轴于点H，得到矩形，求矩形的周长的最大值；

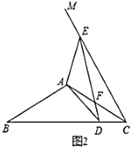
（3）如图2，点为抛物线对称轴上一点，是否存在点，使以点、、为顶点的三角形是直角三角形？若存在，求出点的坐标；若不存在，请说明理由.

Answer 1

【答案】（1），顶点坐标；（2）周长的最大值为；（3）存在，P的坐标为，，，.

【解析】

（1）把A、B坐标代入y=-x2+bx+c，解方程组求出b、c的值即可得答案；（2）设矩形的周长为，，分别讨论-7<x<-3时和-3<x<-2时两种情况，用x表示出矩形的周长，根据二次函数的性质求出最大值即可得答案；（3）设分时，时，时，三种情况讨论，利用勾股定理求出m的值即可得答案.

（1）把两点坐标代入

得，

解得：，

∴抛物线方程为：，顶点坐标，

（2）

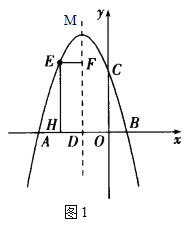
如图1，设矩形的周长为，，

∴，

∵A（-7，0），B（1，0），

∴抛物线对称轴为直线x=-3，

①当时，

，

，

=

=

=

=

∵，

∴时，矩形周长最大，最大值为.

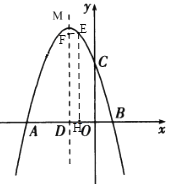
②当时

EF=x-(-3)=x+3，

l=

=

.

∴当时，矩形周长最大，最大值为

∴综上所述，周长的最大值为

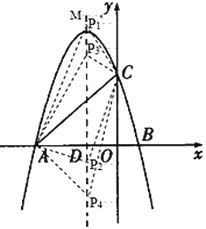
（3）存在.如下图

设

（i）当时，

16+

16

2

m2

解得：

∴P1，P2

（ii）当时，

49+49+9+(7-m)2=16+m2

∴

140=14m，

m=10，

∴P3，

（iii）当时，

98+16+m2=9+(7-m)2

49+49+16+m2=9+49-14m+m2

56=-14m

解得：，

∴P4

综上所述：满足条件的点P的坐标为，，，