��Ŀ����
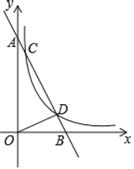
����Ŀ���ƻ�С˵��ʵ���ҵĹ��¡��У�������һ����ڣ���ѧ�Ұ�һ�������ֲ��ֱ���ڲ�ͬ�¶ȵĻ����У�����һ����Գ�����ֲ��߶ȵ�����������������
�¶� | ���� |
|
| 0 | 2 | 4 | 4.5 | ���� |
ֲ��ÿ��߶������� | ���� | 41 | 49 | 49 | 41 | 25 | 19.75 | ���� |
����Щ���ݣ���ѧ���Ʋ��ֲ��ÿ��߶�������![]() ���¶�
���¶�![]() �ĺ����������ֺ�����һ�κ����Ͷ��κ����е�һ�֣�
�ĺ����������ֺ�����һ�κ����Ͷ��κ����е�һ�֣�
��1������ѡ��һ���ʵ��ĺ�����������ĺ�����ϵʽ������Ҫ˵����ѡ������һ�ֺ��������ɣ�
��2�����ʵ�����¶ȱ��ֲ��䣬��10����Ҫʹ��ֲ��߶����������ܺͳ���![]() ����ôʵ���ҵ��¶�
����ôʵ���ҵ��¶�![]() Ӧ�����ĸ���Χ��ѡ����˵�����ɣ�
Ӧ�����ĸ���Χ��ѡ����˵�����ɣ�
���𰸡���1��ѡ����κ�����![]() �����ɼ���������2��-6�棼x��4�棬���ɼ�����
�����ɼ���������2��-6�棼x��4�棬���ɼ�����
��������
��1��ѡ����κ�������y=ax2+bx+c��a��0����Ȼ��ѡ��x=-2��0��2�������ݣ����ô���ϵ��������κ�������ʽ���ɣ��ٸ���һ�κ����ĵ㶼��һ��ֱ�����ų�һ�κ�����
��2�����ƽ��ÿ��ĸ߶�������Ϊ25mm��Ȼ�����y=25���x��ֵ���ٸ��ݶ��κ���������д��x��ȡֵ��Χ���ɣ�
�⣺��1��ѡ����κ�������![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��![]() ʱ��
ʱ��![]() ��
��![]() ʱ��
ʱ��![]() ��
��
�� �����
����� ��
��
���ԣ�![]() ����
����![]() �ĺ�����ϵʽΪ
�ĺ�����ϵʽΪ![]() ��
��
��ѡ����һ�����������ɣ�
�ߵ�![]() ��
��![]() ��
��![]() ����ͬһֱ���ϣ�
����ͬһֱ���ϣ�
��![]() ����
����![]() ��һ�κ�����
��һ�κ�����
��2����10����Ҫʹ��ֲ��߶����������ܺͳ���![]() ��
��
��ƽ��ÿ���ֲ��߶�����������![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
�����ã�![]() �����
�����![]() ��
��![]() ��
��
����10����Ҫʹ��ֲ��߶����������ܺͳ���![]() ��ʵ���ҵ��¶�Ӧ������-6�棼x��4��.
��ʵ���ҵ��¶�Ӧ������-6�棼x��4��.

����Ŀ������1��ʼ��������Ȼ����ͼ�������У�
�� �� | ��1�� | ��2�� | ��3�� | ��4�� |
��1�� | 1 | 2 | 3 | 4 |
��2�� | 8 | 7 | 6 | 5 |
��3�� | 9 | 10 | 11 | 12 |
��4�� | 16 | 15 | 14 | 13 |
�� | �� | �� | �� | �� |
�� | �� | �� | �� | �� |
�涨λ�ڵ�![]() �У���
�У���![]() �е���Ȼ��10��Ϊ
�е���Ȼ��10��Ϊ![]() ����Ȼ��15��Ϊ
����Ȼ��15��Ϊ![]() �����˹��ɣ���Ȼ��2018��Ϊ______��
�����˹��ɣ���Ȼ��2018��Ϊ______��