题目内容
(1)平面内2条直线交点有几个交点?3条直线相交有几个交点(每个交点都不经过第3条直线)?4条直线相交有几个交点?(每3条直线不共点)?5条直线相交有几个交点(每3条直线不共点)?
(2)请探索n条直线相交的交点个数(每3条直线不共点).
(2)请探索n条直线相交的交点个数(每3条直线不共点).
考点:相交线
专题:规律型
分析:(1)两条直线只有1个交点,
第3条直线和前两条直线都相交,增加了2个交点,得1+2,
第4条直线和前3条直线都相交,增加了3个交点,得1+2+3,
第5条直线和前4条直线都相交,增加了4个交点,得1+2+3+4,
(2)根据(1)即可得出第n条直线和前n-1条直线都相交,增加了多少个交点,以及这些交点的总数.
第3条直线和前两条直线都相交,增加了2个交点,得1+2,
第4条直线和前3条直线都相交,增加了3个交点,得1+2+3,
第5条直线和前4条直线都相交,增加了4个交点,得1+2+3+4,
(2)根据(1)即可得出第n条直线和前n-1条直线都相交,增加了多少个交点,以及这些交点的总数.
解答:解:(1)平面内2条直线交点有1个交点,
第3条直线和前两条直线都相交,增加了2个交点,得1+2=3个交点,
第4条直线和前3条直线都相交,增加了3个交点,得1+2+3=6个交点,
第5条直线和前4条直线都相交,增加了4个交点,得1+2+3+4=10个交点;
(2)第n条直线和前n-1条直线都相交,增加了n-1个交点,得1+2+3+…n-1,
其和为:1+2+3+…n-1=
n(n-1)个交点.
第3条直线和前两条直线都相交,增加了2个交点,得1+2=3个交点,
第4条直线和前3条直线都相交,增加了3个交点,得1+2+3=6个交点,
第5条直线和前4条直线都相交,增加了4个交点,得1+2+3+4=10个交点;
(2)第n条直线和前n-1条直线都相交,增加了n-1个交点,得1+2+3+…n-1,
其和为:1+2+3+…n-1=
| 1 |
| 2 |
点评:本题考查的是多条直线相交的交点问题,解答此题的关键是找出规律,即n条直线相交有
n(n-1)个交点.
| 1 |
| 2 |

练习册系列答案
相关题目
甲上午6时步行从A地出发于下午5时到达B地,乙上午10时骑自行车从A地出发于下午3时到达B地,则乙追上甲的时间为( )
| A、12时20分 |
| B、13时20分 |
| C、14时20分 |
| D、11时20分 |
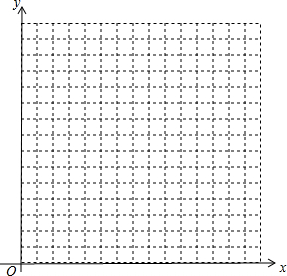 在下面的直角坐标系中描出下列各点,顺次用线段将下面各点连起来,并将最后一点与第一点连接起来,看看得到的是一个什么图形?(2,2),(5,2),(7,0),(9,2),(12,2),(12,5)(14,7),(12,9),(12,12),(9,12),(7,14),(5,12),(2,12),(2,9),(0,7),(2,5)
在下面的直角坐标系中描出下列各点,顺次用线段将下面各点连起来,并将最后一点与第一点连接起来,看看得到的是一个什么图形?(2,2),(5,2),(7,0),(9,2),(12,2),(12,5)(14,7),(12,9),(12,12),(9,12),(7,14),(5,12),(2,12),(2,9),(0,7),(2,5) 如图,菱形ABCD中,AB=4,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为
如图,菱形ABCD中,AB=4,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为