题目内容
4.某商场经销一种销售成本为每千克30元的水产品,据市场调查,如果按每千克40元销售,一周能售出500千克;销售单价每提高2元,每周销售量就减少20千克,(1)销售单价定为多少元时,每周的销售利润最大?最大利润是多少元?
(2)商店在周销售成本不超过10000元的情况下,要使周销售利润达到8000元,销售单价应定为多少元?
分析 (1)设销售单价为x元,销售利润为S,则销售量为[500-10(x-40)]件.根据题意构建二次函数,利用二次函数的性质即可解决问题.
(2)列出方程,求出x的值,再判断销售成本是否符合题意即可.
解答 解:(1)设销售单价为x元,销售利润为S,则销售量为[500-10(x-40)]件.
S=(x-30)(900-10x)=-10x2+1200x-27000=-10(x-60)2+9000
当50≤x≤60时,利润随着单价的增大而增大.
当单价定位60元时,利润最大为9000元.
答:单价定位60元时,利润最大为9000元.
(2)设销售单价为x元,则销售量为[500-10(x-40)]件,由题意得
(x-30)[500-10(x-40)]=8000
整理,得x2-120x+3500=0,即-(x-50)(x-70)=0,
解得 x1=50,x2=70
当x=50时,成本=30×[500-10(50-40)]=12000<10000不符合要求,舍弃.
当x=70时,成本=30×[500-10(70-40)]=6000<10000符合要求.
销售单价应定为70元,才能使得一周销售利润达到8000元的同时,投入不超过10000元.
答:销售单价定为70元;
点评 此题主要考查了二次函数的应用以及用配方法求出最大值,准确分析题意,列出y与x之间的二次函数关系式是解题关键.

练习册系列答案
相关题目
 如图,在Rt△ABC中,AB=AC=4$\sqrt{2}$.一动点P从点B出发,沿BC方向以每秒1个单位长度的速度匀速运动,到达点C即停止.在整个运动过程中,过点P作PD⊥BC与Rt△ABC的直角边相交于点D,以PD为直角边在PD左侧作等腰直角三角形PDE.在整个运动过程中,设△ABC与△PDE重叠部分的面积为S,设运动时间为t秒.
如图,在Rt△ABC中,AB=AC=4$\sqrt{2}$.一动点P从点B出发,沿BC方向以每秒1个单位长度的速度匀速运动,到达点C即停止.在整个运动过程中,过点P作PD⊥BC与Rt△ABC的直角边相交于点D,以PD为直角边在PD左侧作等腰直角三角形PDE.在整个运动过程中,设△ABC与△PDE重叠部分的面积为S,设运动时间为t秒. 在如图所示的方格纸中,每个小正方形方格的边长都为1,△ABC的三个顶点在格点上.
在如图所示的方格纸中,每个小正方形方格的边长都为1,△ABC的三个顶点在格点上. 如图所示,正方形OABC的两边OA,OC分别在x轴、y轴上,点D(5,3)在边AB上,以点C为中心,把△CDB旋转90°.
如图所示,正方形OABC的两边OA,OC分别在x轴、y轴上,点D(5,3)在边AB上,以点C为中心,把△CDB旋转90°. 如图,直线CD与直线AB相交于C,根据下列语句画图
如图,直线CD与直线AB相交于C,根据下列语句画图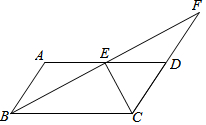 如图,在四边形ABCD中,AB∥CD,AD∥BC,AB=CD,AD=BC,点E是AD的中点,连接BE并延长交CD的延长线于点F.
如图,在四边形ABCD中,AB∥CD,AD∥BC,AB=CD,AD=BC,点E是AD的中点,连接BE并延长交CD的延长线于点F.