题目内容
13.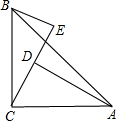 如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于点D,AD=3.1cm,DE=1.8cm,求BE的长.
如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于点D,AD=3.1cm,DE=1.8cm,求BE的长.
分析 根据AAS证明△ACD≌△CBE,再利用其性质解答即可.
解答 证明:∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
∵AD⊥CE,BE⊥CE,
∴∠ADC=∠CEB=90°,∠CAD+∠ACD=90°,
∴∠BCE=∠CAD,
在△ACD与△CBE中,
$\left\{\begin{array}{l}{∠ADC=∠CEB}\\{∠BCE=∠CAD}\\{AC=BC}\end{array}\right.$,
∴△ACD≌△CBE,
∴BE=CD,CE=AD,
∴BE=CD=CE-DE=AD-DE=3.1-1.8=1.3cm.
点评 本题考查三角形全等的判定和性质,要根据AAS证明△ACD≌△CBE是解题的关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
8.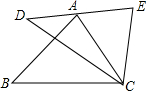 如图,点A在DE上,AC=CE,∠DAB=∠BCD=∠ACE,则AB与DE的数量关系为( )
如图,点A在DE上,AC=CE,∠DAB=∠BCD=∠ACE,则AB与DE的数量关系为( )
 如图,点A在DE上,AC=CE,∠DAB=∠BCD=∠ACE,则AB与DE的数量关系为( )
如图,点A在DE上,AC=CE,∠DAB=∠BCD=∠ACE,则AB与DE的数量关系为( )| A. | AB=DE | B. | AB>DE | C. | AB<DE | D. | 不能确定 |
5.下列计算的结果正确的是( )
| A. | a+a=a2 | B. | a4-a2=a2 | C. | 3a+b=3ab | D. | a2-3a2=-2a2 |
 尺规作图:请作出线段AB的垂直平分线CD,并说明作图依据.
尺规作图:请作出线段AB的垂直平分线CD,并说明作图依据.
 已知A(0,4)、B(6,2)表示两个村庄的位置,x轴表示公路的位置,请你在x轴上求一点P,使得AP+BP最小.
已知A(0,4)、B(6,2)表示两个村庄的位置,x轴表示公路的位置,请你在x轴上求一点P,使得AP+BP最小.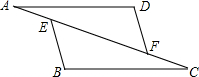 如图,已知:AD∥BC,AD=CB,AE=CF.求证:∠D=∠B.
如图,已知:AD∥BC,AD=CB,AE=CF.求证:∠D=∠B.