Question

11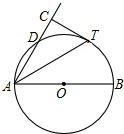．如图，AB是⊙O直径，D为⊙O上一点，AT平分∠BAD交⊙O于点T，过T作AD的垂线交AD的延长线于点C．
（1）求证：CT为⊙O的切线；
（2）连接BT，若⊙O半径为1，AT=$\sqrt{3}$，求BT的长．

Answer 1

分析 （1）连接OT，根据角平分线的性质，以及直角三角形的两个锐角互余，证得CT⊥OT，CT为⊙O的切线；
（2）连接BT，由圆周角定理得出∠ATB=90°，再由勾股定理求出BT即可．

解答 （1）证明：连接OT，如图1所示：
∵OA=OT，
∴∠OAT=∠OTA，
又∵AT平分∠BAD，
∴∠DAT=∠OAT，
∴∠DAT=∠OTA，
∴OT∥AC，
又∵CT⊥AC，
∴CT⊥OT，
∴CT为⊙O的切线；
（2）解：连接BT，如图2所示：
∵AB是⊙O直径，
∴AB=2，∠ATB=90°，
∴BT=$\sqrt{A{B}^{2}-A{T}^{2}}$=$\sqrt{{2}^{2}-（\sqrt{3}）^{2}}$=1．

点评 本题主要考查了切线的判定、等腰三角形的性质、平行线的判定、圆周角定理、勾股定理；熟练掌握切线的判定和圆周角定理是解决问题的关键．